5장: SVM(서포트 벡터 머신) (p.201)
Support Vector Machine
이번 part에선 신경망이 활황을 이루기전 가장 강력한 머신러닝 모델로써 그 원리와 사용방법에 대해 공부하고자 한다.
Support Vector Machine 이론 :


쌍대 형식으로의 표현과 좀더 일반화 시킨 방법인 소프트 마진 방법, 마지막으로 비선형 분류(kernel trick 등) 의 이론은 나중에 더 공부해보기로.
Support Vector Machine 개념
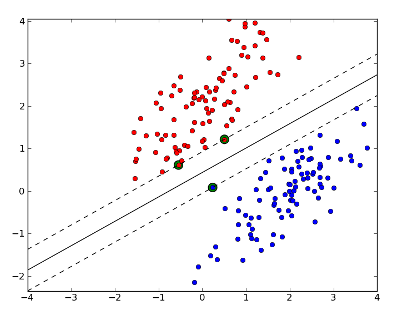
선형 SVM 분류

데이터들의 집합을 가장 잘 선형적으로 분리해보고자 하는 아이디어에서 시작하여 서포트 벡터들을 기준으로 margin이 최대가 되는 도로를 구하는 것이다. (서포트 벡터 주위에 다른 데이터들이 생겨도 잘 분류하기 위해서)
1.hard margin classification
모든 샘플이 잘 몰려 있어서 구분이 이상치없이 잘 분류되어 있는 경우를 말한다. 하지만 두 가지 문제점이 존재하는데 첫 째, 데이터가 선형적으로 구분될 수 있어야 제대로 작동하며, 둘 째, 이상치에 민감하다.
2.Soft margin classification
위의 문제를 피하기 위해 좀 더 유연한 모델이다. (margin 폭을 가능한 한 넓게 유지하는 것과 margin violation(마진 오류) 사이에 적절한 균형을 잡아야 한다. ) 사이킷 런의 SVM 모델에서는 이를 C 하이퍼파라미터로 조절할 수 있다. C 값을 줄이면 도로의 폭이 넓어지지만 마진 오류도 커진다.
(SVM 모델이 과대적합이라면 C를 감소시켜 모델을 규제할 수 있다.)
비선형 SVM 분류
자세히 다루지 않고 조금만 개념맛보기
선형적으로 분류할 수 없는 데이터셋을 다루는 한 가지 방법으론 다항 특성과 같은 특성을 더 추가하는 것이 있다.

다항 특성을 사용한 선형 SVM 분류기
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
#비선형 SVM 분류 X,y = make_moons(n_samples=100, noise=0.15, random_state=42) polynomial_svm_clf = Pipeline([ ("poly_features", PolynomialFeatures(degree=3)), ("scaler", StandardScaler()), ("svm_clf", LinearSVC(C=10, loss="hinge")) ]) polynomial_svm_clf.fit(X,y) def plot_dataset(X, y, axes): plt.plot(X[:, 0][y==0], X[:, 1][y==0], "bs") plt.plot(X[:, 0][y==1], X[:, 1][y==1], "g^") plt.axis(axes) plt.grid(True, which='both') plt.xlabel(r"$x_1$", fontsize=20) plt.ylabel(r"$x_2$", fontsize=20, rotation=0) def plot_predictions(clf, axes): x0s = np.linspace(axes[0], axes[1], 100) x1s = np.linspace(axes[2], axes[3], 100) x0, x1 = np.meshgrid(x0s, x1s) X = np.c_[x0.ravel(), x1.ravel()] y_pred = clf.predict(X).reshape(x0.shape) y_decision = clf.decision_function(X).reshape(x0.shape) plt.contourf(x0, x1, y_pred, cmap=plt.cm.brg, alpha=0.2) plt.contourf(x0, x1, y_decision, cmap=plt.cm.brg, alpha=0.1) plot_predictions(polynomial_svm_clf, [-1.5, 2.5, -1, 1.5]) plot_dataset(X, y, [-1.5, 2.5, -1, 1.5]) plt.show() |

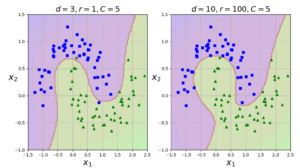
다항식 커널
다항식 특성을 추가하는 것은 매우 많은 계산량을 필요로 한다. kernel trick 을 사용하면 실제로 특성을 추가하지 않으면서 다항식 특성을 많이 추가한 것과 같은 결과를 얻을 수 있다.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
#다항식 커널 poly_kernel_svm_clf = Pipeline([ ("scaler", StandardScaler()), ("svm_clf", SVC(kernel="poly", degree=3, coef0=1, C=5)) ]) poly_kernel_svm_clf.fit(X, y) poly100_kernel_svm_clf = Pipeline([ ("scaler", StandardScaler()), ("svm_clf", SVC(kernel="poly", degree=10, coef0=100, C=5)) ]) poly100_kernel_svm_clf.fit(X, y) plt.figure(figsize=(11, 4)) plt.subplot(121) plot_predictions(poly_kernel_svm_clf, [-1.5, 2.5, -1, 1.5]) plot_dataset(X, y, [-1.5, 2.5, -1, 1.5]) plt.title(r"$d=3, r=1, C=5$", fontsize=18) plt.subplot(122) plot_predictions(poly100_kernel_svm_clf, [-1.5, 2.5, -1, 1.5]) plot_dataset(X, y, [-1.5, 2.5, -1, 1.5]) plt.title(r"$d=10, r=100, C=5$", fontsize=18) plt.show() |
가우시안 RBF를 사용한 유사도 특성

RBF 커널을 사용한 SVM 분류기

하이퍼 파라미터 gamma 값이 규제의 역할을 한다.
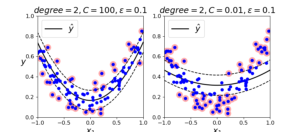
SVM회귀
SVM 회귀는 분류와 목적을 반대로 하면 된다. 일정한 margin 오류 안에서 두 클래스 간의 도로 폭이 가능한 한 최대가 되도록 많은 샘플이 들어가도록 학습한다. 도로의 폭은 하이퍼파라미터 ε 으로 조절한다.

비선형 회귀 작업을 처리하려면 커널 SVM 모델을 사용한다.
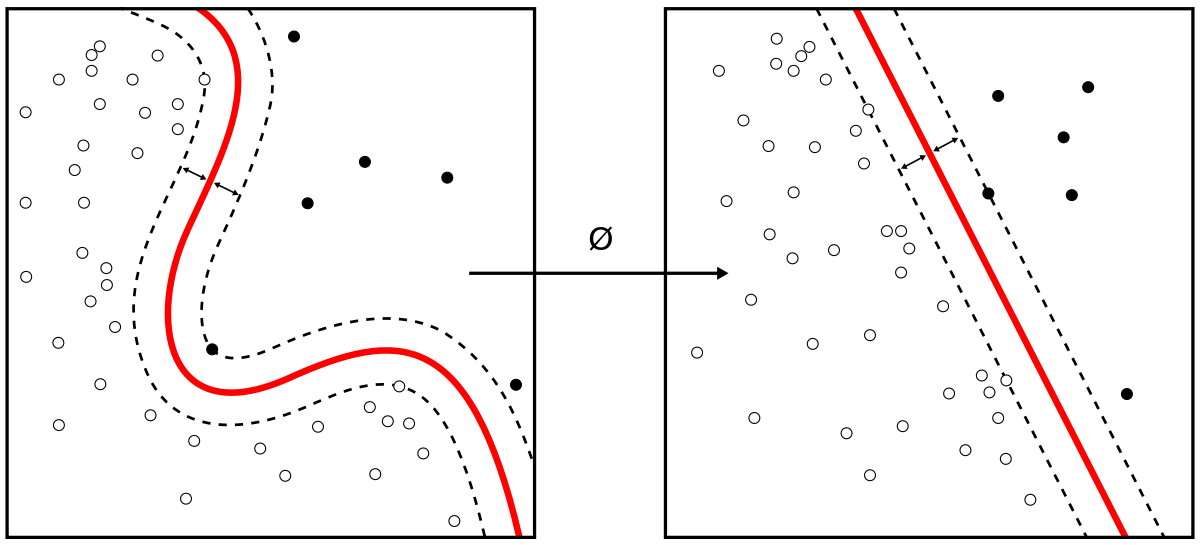
Kernel Trick
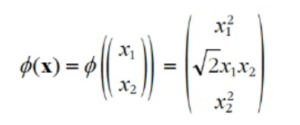
예를 들어 2차원 데이터셋에 2차 다항식 변환을 적용하고 선형 SVM 분류기를 변환된 이 훈련 세트에 적용한다고 하자. 우리가 적용하고자 하는 2차 다항식 매핑 함수 이다. 변환된 벡터는 2차원에서 3차원이 된다.

변환된 벡터의 점곱이 원래 벡터의 점곱의 제곱과 같다. 전체 과정에 필요한 계산량 측면에서 엄청 효율적이다. 이것이 Kernel trick이다.
Reference : Hands – On Machine Learning with Scikit-Learn & TensorFlow

 이다. 변환된 벡터는 2차원에서 3차원이 된다.
이다. 변환된 벡터는 2차원에서 3차원이 된다.