M.L (p.131)
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
import numpy as np from p88func import * def gradient_descent(f, init_x, lr=0.01, step_num=100): x = init_x for i in range(step_num): grad = numerical_gradient(f,x) x -= lr * grad return x def function_2(x): return x[0]**2 + x[1]**2 init_x = np.array([-3.0,4.0]) d = gradient_descent(function_2,init_x=init_x,lr=0.1,step_num=100) print(d) init_x = np.array([-3.0,4.0]) print(gradient_descent(function_2,init_x=init_x, lr = 10.0, step_num=100)) init_x = np.array([-3.0,4.0]) print(gradient_descent(function_2,init_x=init_x, lr = 1e-10, step_num=100)) |
gradient_descent method 로

![]() (eta) 는 갱신하는 양을 나타내고 신경망에서는 이를 학습률(learning rate)라 부른다. 이 parameter는 사용자가 정의하며 learning rate * 편미분 값 을 기존 변수 값에서 빼는 단계를 여러번 반복하는 것이 경사하강법이다.
(eta) 는 갱신하는 양을 나타내고 신경망에서는 이를 학습률(learning rate)라 부른다. 이 parameter는 사용자가 정의하며 learning rate * 편미분 값 을 기존 변수 값에서 빼는 단계를 여러번 반복하는 것이 경사하강법이다.
 learning_rate ( lr= 0.01) 로 맞추어 놓은 후 그래프로 보면 최적값에 매우 근접하게 도달한 것을 알 수 있다. 하지만 lr 값이 10 이거나 1e-10등 크거나 작은 학습률을 사용하게 되면 값이 발산하거나 아예 제자리 걸음을 하는 듯한 모습을 보여줄 수도 있다.
learning_rate ( lr= 0.01) 로 맞추어 놓은 후 그래프로 보면 최적값에 매우 근접하게 도달한 것을 알 수 있다. 하지만 lr 값이 10 이거나 1e-10등 크거나 작은 학습률을 사용하게 되면 값이 발산하거나 아예 제자리 걸음을 하는 듯한 모습을 보여줄 수도 있다.
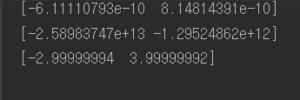
lr = 0.01 두 값이 0에 가까운 최적 값에 근접함
lr = 10 일때 매우 큰 값으로 발산
lr = 1e-10 일때 미동이 없음