M.L (p.206)
가중치의 초깃값 중 Xavier – 초깃값에 대해
앞서 우리는 data의 distribution이 gradient vanishing 문제와 표현력을 제한하는 문제에 대해 알아보았다. 이를 통해 data의 distribution이 광범위하게 골고루 분포되어 있어야 효율적인 학습을 할 수 있다는 것을 알았다.
그 중 하나의 방법인 Xavier- 초깃값에 대해 간단히 알아보겠다.
기본적인 아이디어는 층에 따른 노드의 개수에 영향을 받아 사용하는 방법이다.
앞 계층의 노드가 n개 라면 표준편차가 1 / 루트n 인 분포를 사용하면 된다고 한다. 앞서 node의 개수는 100개이고 Xavier-초깃값과 sigmoid function을 사용한 결과는 다음과 같다.
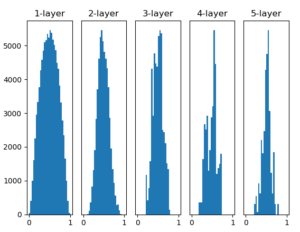
앞서 본 방식보다는 데이터의 분포가 그나마 봐줄만 하다.
Data의 distribution을 자꾸만 건드는 이유 : (Sigmoid 함수로 설명)
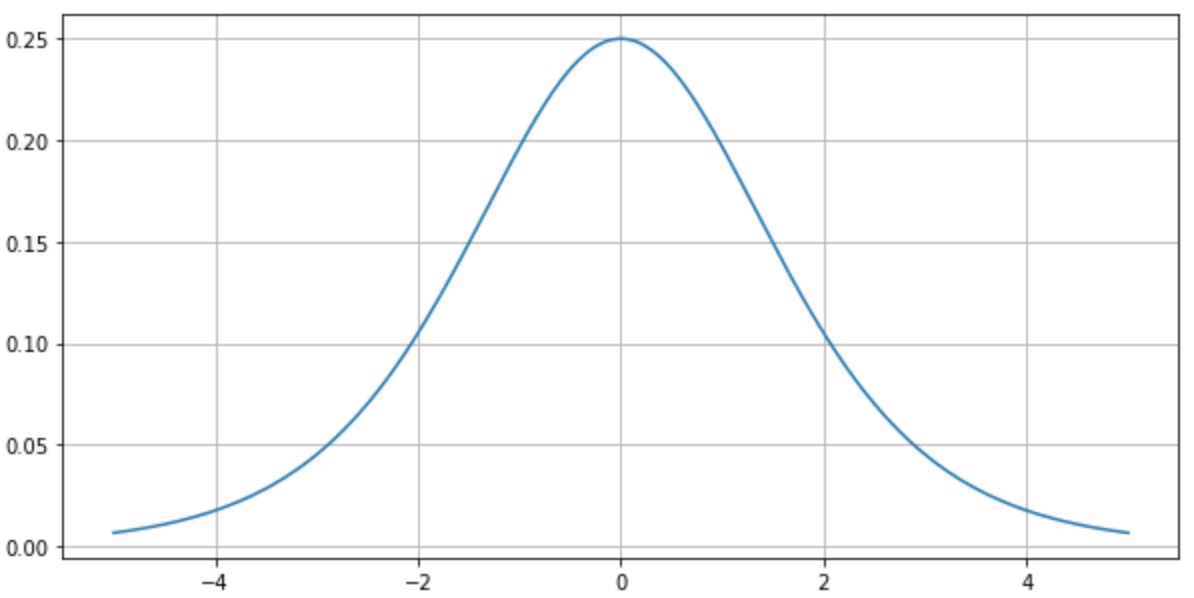
backpropagation 과정에서 sigmoid를 미분한 연산이 작용하는데 위 그림을 보면 알다시피 미분에 최대계수가 0.25이다. 우리가 직면하는 어떤 문제에 대한 data는 방대한 범위일 수 있는데 이것을 최대 미분계수가 0.25인 function에 집어넣는 행위는 어리석은 행위로 보일 수 밖에 없다. 얘기의 논점은 이 부분이 아니므로 생략한다.
1. 가중치 초깃값을 표준편차가 1인 정규분포로 그대로 주는 경우
sigmoid로 연산 했을 때 data가 0과 1에 쏠리므로 아래의 그래프 처럼 분포하게 된다.
이는 즉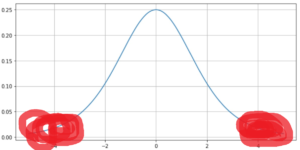 
색칠한 부분에 data가 분포되어 있으므로 오차역전파를 시행할 경우 학습이 전혀 되지 않는 gradient vanishing 문제에 직면한다.
2. 초깃값을 0.01로 곱해서 준다면(작게 준다면?)
sigmoid 연산 후에 data의 분포를 보면 0.5 중간 값에 매우 밀집되어 있는 형태를 볼 수 있다. 이는 표현력 제한이라는 문제인데 집중적으로 아주 작은 범위를 가리키는 데이터들의 분포는 학습을 해봐야 같은 것을 학습하기에 필요가 없다 (앞전의 게시글 참고)
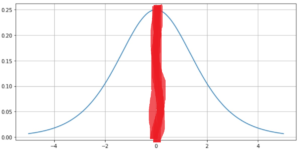
오차역전파로 보면 0.01 곱으로 초기화된 데이터는 표시된 0.5부분에 집중적으로 밀집되어 있기 때문에 data 갯수가 많아도 같은 것을 학습한다고 할 수 있다.
3. sigmoid에 좋다고 알려진 Xavier 초깃값
맨 위의 그래프처럼 Xavier는 층의 노드 수 만큼의 영향을 받는 함수이므로 data가 적당히 분포되게 도움을 준다.
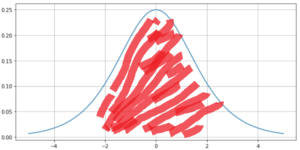
노드의 표준편차만큼 나눠주기 때문에 데이터의 분포가 sigmoid 미분 그래프에서 보면 비교적 골고루 퍼져있어서 학습에 용이하게 보인다.
결론(Conclusion) :
activation function들을 미분했을 때의 분포에서 data들을 자꾸만 그 분포에 잘 맞게 변형을 시켜줘야 한다. ( 이동을 하든 범위를 좁히든 )
