케라스에서 epoch안의 step에서 train data와 test data는 어떻게 계산되는가?
keras :
60,000개의 학습데이터를 섞지 않고 128개의 batch 크기, 2 epoch 을 step 당 계산

python :
python도 마찬가지로 같은 구조의 같은 파라미터 초기화, (같은 순서 아닌지 확인해야함)같은 순서의 데이터세트를 사용하여 step 마다 60,000개의 데이터에 대해 손실함수를 평가
결과 그림 :
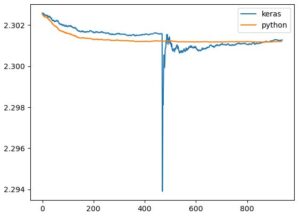
python에서 batch 128개 마다 학습 후 계산한 것:

학습 데이터의 셔플 순서 같음 확인
python cross-entropy 와 keras cross-entropy 비교


=================================================Iris data 실험=====================
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
import os os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2' from LossHistory import * from data_load import load_mnist from NNClass.nnclass import * from NNClass.neural_nework_class import * import sys import numpy as np from tensorflow.keras.models import Model import matplotlib.pyplot as plt from sklearn.datasets import load_iris from keras.utils import np_utils X_data = load_iris()['data'] y_data = load_iris()['target'] y_data = np_utils.to_categorical(y_data) print(len(X_data)) print(y_data[:5]) path = "D:\\PycharmProjects\\Keras_NN\\model\\Iris\\" batch_size = 150 epochs = 6 model = Iris_run() model.compile(optimizer='sgd', loss='categorical_crossentropy', metrics=['accuracy']) loss = Loss(model=model, save_path=path, step_per=False) model.fit(x=X_data, y=y_data, batch_size=batch_size, epochs=epochs, steps_per_epoch=1, verbose=1, validation_data=False, callbacks=[loss]) loss.save_result() |
|
1 2 3 4 5 6 7 |
class Iris_run(Model): def __init__(self): super(Iris_run, self).__init__() self.dense = layers.Dense(3, kernel_initializer='Ones', activation='softmax') def call(self, inputs, training=None, mask=None): return self.dense(inputs) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
import numpy as np import sys import os import matplotlib.pyplot as plt import tensorflow as tf import keras from NNClass.neural_nework_class import * from Full_code import * os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2' from data_load import load_mnist from mnist_cnn_clf import * from sklearn.datasets import load_iris from keras.utils import np_utils path = "D:\\PycharmProjects\\Keras_NN\\model\\Iris\\" loss = np.load(path + "loss.npy", allow_pickle=True).tolist() keras_train_loss = loss['train_loss'] print(keras_train_loss) print(len(keras_train_loss)) #plt.plot(np.arange(len(keras_train_loss)), keras_train_loss) #plt.show() X_data = load_iris()['data'] y_data = load_iris()['target'] y_data = np_utils.to_categorical(y_data) print(y_data[:5]) key_list = [] key_list.append('W1') key_list.append('b1') network = IrisNet() |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
loss_list = [] loss_list.append(network.loss(X_data,y_data)) print(network.loss(X_data,y_data)) for epoch in range(5): grad = network.gradient(X_data,y_data) for key in key_list: network.params[key] -= 0.01 * grad[key] print(epoch, "th loss :", network.loss(X_data,y_data)) loss_list.append(network.loss(X_data,y_data)) plt.plot(np.arange(len(keras_train_loss)), keras_train_loss, label='keras') plt.plot(np.arange(len(loss_list)), loss_list, label='python', alpha=0.5) plt.legend() plt.show() |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 |
class IrisNet: """완전연결 다층 신경망 Parameters ---------- input_size : 입력 크기(MNIST의 경우엔 784) hidden_size_list : 각 은닉층의 뉴런 수를 담은 리스트(e.g. [100, 100, 100]) output_size : 출력 크기(MNIST의 경우엔 10) activation : 활성화 함수 - 'relu' 혹은 'sigmoid' weight_init_std : 가중치의 표준편차 지정(e.g. 0.01) 'relu'나 'he'로 지정하면 'He 초깃값'으로 설정 'sigmoid'나 'xavier'로 지정하면 'Xavier 초깃값'으로 설정 weight_decay_lambda : 가중치 감소(L2 법칙)의 세기 """ def __init__(self): self.params = OrderedDict() self.__init_weight() # self.layers = OrderedDict() self.layers['Affine1'] = Affine(self.params['W1'], self.params['b1']) self.last_layer = SoftmaxWithLoss() def __init_weight(self): self.params['W1'] = np.ones((4,3)) self.params['b1'] = np.zeros((3,)) def predict(self, x): for layer in self.layers.values(): x = layer.forward(x) return x def loss(self, x, t): """손실 함수를 구한다. Parameters ---------- x : 입력 데이터 t : 정답 레이블 Returns ------- 손실 함수의 값 """ y = self.predict(x) return self.last_layer.forward(y, t) def accuracy(self, x, t): y = self.predict(x) y = np.argmax(y, axis=1) #index를 뱉어 if t.ndim != 1: t = np.argmax(t, axis=1) accuracy = np.sum(y == t) / float(x.shape[0]) """ t = np.array(np.reshape(t, (-1, 1)), dtype=np.float32) y = self.predict(x) y_copy = np.zeros_like(y) y_copy[np.where(y > 0.5)] = 1. accuracy = np.sum(y_copy == t) / float(len(x)) """ return accuracy def gradient(self, x, t): """기울기를 구한다(오차역전파법). Parameters ---------- x : 입력 데이터 t : 정답 레이블 Returns ------- 각 층의 기울기를 담은 딕셔너리(dictionary) 변수 grads['W1']、grads['W2']、... 각 층의 가중치 grads['b1']、grads['b2']、... 각 층의 편향 """ # forward self.loss(x, t) # backward dout = 1 dout = self.last_layer.backward(dout) layers = list(self.layers.values()) # list로 만들어줘야 가능 layers.reverse() for layer in layers: dout = layer.backward(dout) # 결과 저장 grads = OrderedDict() grads['W1'] = self.layers['Affine1'].dW grads['b1'] = self.layers['Affine1'].db return grads |
Epoch 당 계산은 맞음

paper hexpo 와 paper relu는 같은 초기화 값을 사용하였고 keras relu는 다른 초기화값을 사용한 것