정규방정식의 명시적인 해를 사용하지 않고 gradient descent를 사용하는 이유
우리가 풀고자 하는 실제 문제가 인 선형식일 것이라 가정한 뒤 선형식에 맞지 않는 error(오차)를
로 두었다. 문제를 선형식으로 가정해놓고
이라는 가정을 취한다.
라는 모델을 만들어볼 수 있고
인 가정을 취하면서 (불편 추정량) 이 된다.
data가 선형독립일 경우 이는 선형대수학에서 정규방정식 명시적인 해인
를 구할 수 있다. 문제는 이렇게 곧 잘 풀릴 것처럼 보이는데 왜 정규방정식을 사용하지 않고 gradient descent를 사용할까 ?
data가 선형 독립인가? : 실제 문제를 다룰 때 주어지는
를 구하기 어렵다 ? : 역행렬을 비교적 간단히 구하는 공식들이 존재하나 역행렬을 구하는 과정에서 수치적으로 오차가 발생한다. (조건수) , 반올림오차에 대해 자세히 공부한거 올리기
더 많은 이유가 있겠지만 나중에 더 알아보기로 한다. 이런 이유들 때문에 정규방정식을 사용하지 않고 gradient descent를 사용한다. 특히 gradient descent 방법은 backpropagation 을 통해(chain rule) 각각의 가중치가 loss 값에 얼마나 영향을 미치는지 쉽게 구할 수 있기 때문에 더 선호된다.
그림 2 (X data 1개만 (1행) 을 가지고 봤을 때)
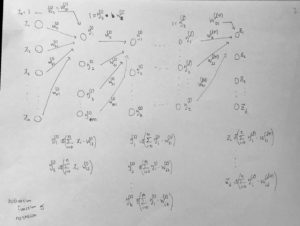
궁금증 : 가 존재한다면 신경망에서 각 노드는
를 구하며 최소제곱해를 구할 수 있을텐데 마지막 최종 노드에 도착해서 목적함수(loss function)을 MSE (mean squared error)로 했을 때, 해 역시
를 만족한다. 그럼 첫 노드부터 올라온
해들은 최종적인 해에 최적해일까?
이 문제는 dynamic system 과 관련이 있으므로 그 분야를 공부해야할 필요가 있음.
{탐욕 알고리즘은 최적해를 구하는 데에 사용되는 근사적인 방법으로, 여러 경우 중 하나를 결정해야 할 때마다 그 순간에 최적이라고 생각되는 것을 선택해 나가는 방식으로 진행하여 최종적인 해답에 도달한다. 순간마다 하는 선택은 그 순간에 대해 지역적으로는 최적이지만, 그 선택들을 계속 수집하여 최종적(전역적)인 해답을 만들었다고 해서, 그것이 최적이라는 보장은 없다.} 와 관련되어 있을까?
그림 3 (X data 관점으로 봤을 때)
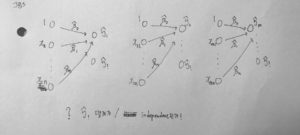
궁금증 : 노드들의 선형 결합으로 나온 노드는 즉 hidden layer 의 노드들은 몇 개이며 층은 몇 층이어야 하나?
같은 hidden layer에 있는 노드들은 independent 한가?
궁금증 : 선형 독립과 통계적 독립은 실제 문제에서 어떤 영향을 미치는가?
