11장: Deep Neural Network (p.353)

개요 :

우리가 사는 세상에서 해결해야 하는 문제는 숫자 맞추기 문제가 아니다. 고해상도의 이미지, 영상에서 수 종의 물체를 감지해야 하는 문제들이다. 이런 문제를 해결하려면 아주 많은 은닉층과 뉴런 수가 필요할 것 같다. 그에 대한 문제도 발생하게 되는데 이런 문제들을 중심으로 이 장을 공부해본다.

vanishing gradient (or exploding gradient) 문제
대규모 신경망에서는 훈련이 극단적으로 느려질 것이다.
수백만 개의 파라미터를 가진 모델은 훈련 세트에 과대적합될 위험이 크다.

Vanishing Gradient / Exploding Gradient

vanishing gradient : gradient descent를 하려고 오차역전파를 하는데 하위층으로 갈수록 기울기가 점점 작아져 아래 층의 가중치는 전혀 학습이 되지 않는 상태

exploding gradient : 반대로 gradient가 점점 커져 여러개의 층이 비정상적으로 큰 가중치로 갱신되면 알고리즘은 발산하게 된다.(순환 신경망에서 자주 발생)

예시 : sigmoid function

ìê·¸ëª¨ì´ë í¨ìì ëí ì´ë¯¸ì§ ê²ìê²°ê³¼

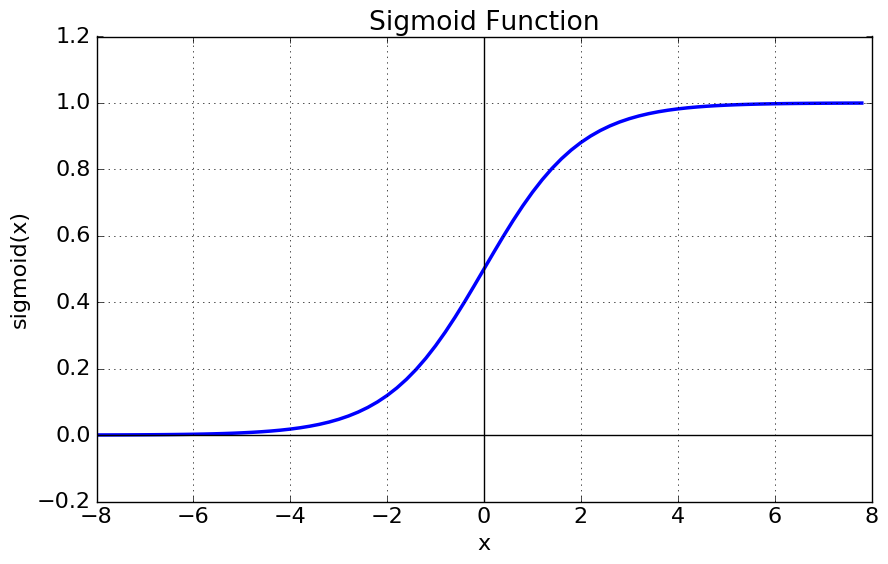
이 sigmoid function을 예로 들자면 이에 대한 미분은 sigmoid(x) = y 라 두었을 때 y(1-y)가 된다.(y의 범위: (0,1) ) 그러므로 y가 0.5일때 가장 큰 미분값을 가지며 그 값은 0.25가 된다.

ìê·¸ëª¨ì´ë í¨ì ë¯¸ë¶ì ëí ì´ë¯¸ì§ ê²ìê²°ê³¼

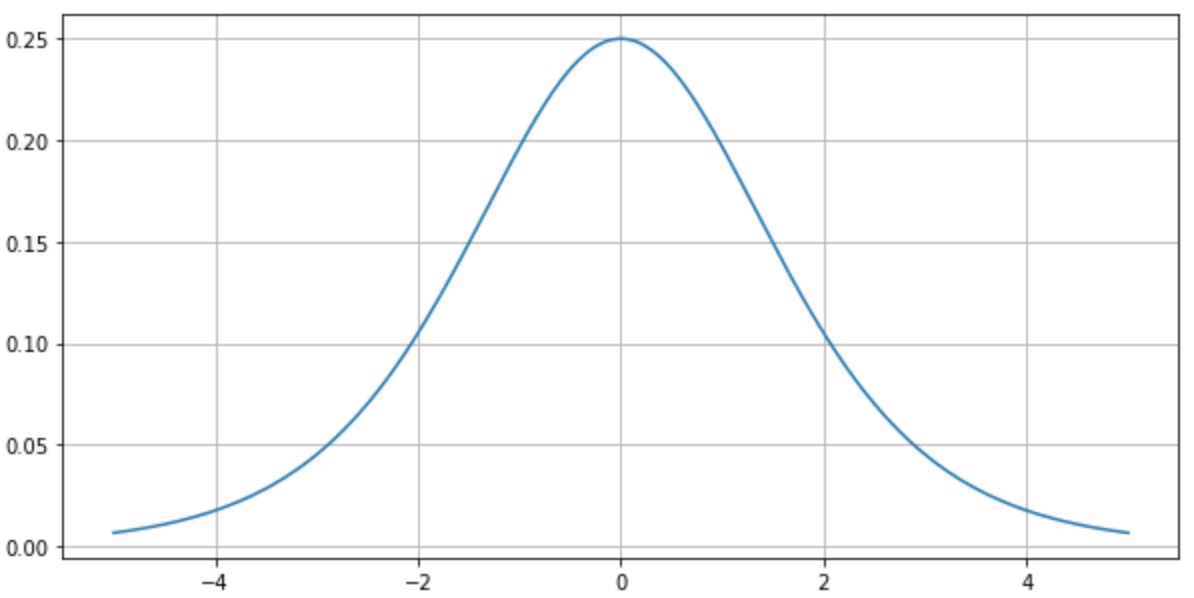
문제는 오차역전파로 진행할 때 이 함수의 미분 값 (0, 0.25)이 곱해져서 전해지는데 1 보다도 현저하게 낮은 0.25가 (이 값이 심지어 제일 큰 값) , 심층신경망에서는 층마다 활성화 함수를 사용하는데 시그모이드 함수를 사용하게 되면 (0, 0.25) 의 값을 매층 마다 곱해지게 되며 이는 결국 0에 가까워지는 아주 작은 값들이 만들어지게 된다. sigmoid 를 사용했을 때 나오는 대표적인 vanishing gradient 문제다.

Xavier Glorot 와 Yoshua Bengio 는 논문을 통해 주요한 발견을 발표했는데 이 중 로지스틱 시그모이드 활성화 함수와 가중치 초기화 방법의 조합이 있다. 이 초기화 방법은 평균이 0 표준편차가 1인 정규분포를 사용한 무작위 초기화이고 시그모이드와 함께 사용했을 때 각 층에서 출력의 분산이 입력의 분산보다 크다는 것을 밝혔다. 신경망의 위쪽으로 갈수록 분산이 계속 커져 활성화 함수가 0 또는 1로 수렴하게 된다. 이 경우 기울기가 0에 가까워지는 것을 위에서 확인했다.

Xavier 초기화, He 초기화

Xavier와 Bengio는 그들의 논문에서 이 문제를 완화시키는 방법을 제안한다. 예측을 할 때는 정방향, 역방향 즉 양방향 신호가 적절하게 흘러야 한다. 이들의 주장은 적절한 신호가 흐르기 위해서는 각 층의 출력에 대한 분산이 입력에 대한 분산과 같아야 한다고 말한다. 그리고 역방향에서 층을 통과하는 전과 후가 그래디언트 분산이 같아야 한다고 주장한다.(기울기가 1로 일정하게) 사실 층의 입력과 출력 연결 개수가 같지 않다면 이 두 가지를 보장할 수 없다. 하지만 이들은 실전에서 잘 작동하는 대안을 제안했다.

각각의 대안들은 정규분포와 균등분포를 따르는 두 가지 방법이 있다.

그림 출처 : https://reniew.github.io/13/

Xavier 초기화

He 초기화

(왜 그러한가에 대해서 나중에 공부하기)

ReLU 함수 중에서도 LeakyReLU 와 ELU

LeakyReLU : ReLU함수에서 0보다 작은 음수의 소실문제를 해결하기 위해 음수에 작은 계수를 곱한 식.

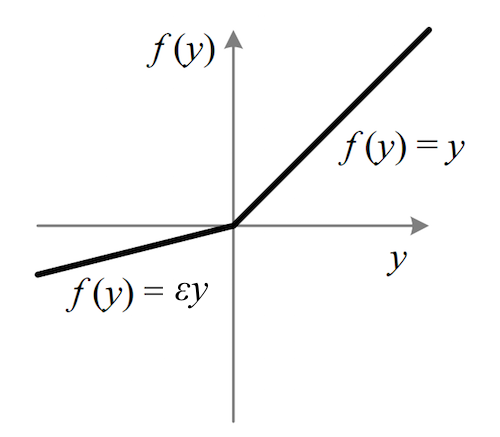
leaky relu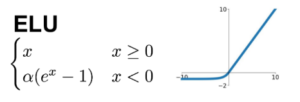ì ëí ì´ë¯¸ì§ ê²ìê²°ê³¼

ELU :

exponential linear unitì ëí ì´ë¯¸ì§ ê²ìê²°ê³¼

Relu 함수와 다른점 :

z < 0 일 때 음수 값이 들어오므로 활성화 함수의 평균 출력이 0에 더 가까워진다. 이는 앞서 이야기한 vanishing gradient 문제를 완화해준다. 하이퍼파라미터 a 는 z가 큰 음수 값일 때 ELU가 수렴할 값을 정의한다. 보통 1로 설정하지만 필요에 따라 달리 정의가능.

z < 0이어도 gradient가 0이 아니기 때문에 dying 뉴런을 만들지 않는다.

a = 1일 때 이 함수는 z = 0에서 급격히 변동하지 않고 z = 0을 포함해 모든 구간에서 매끄러워 gradient descent 속도를 높여준다.

단점 : 지수함수를 사용하기에 다른 ReLU보다 계산이 느리다. 훈련 동안에는 수렴 속도가 빠르기 때문에 상쇄되지만 테스트 시에는 ELU 신경망이 ReLU 신경망보다 느릴 것이다.

* tf.nn.swish() 함수 :

공식 : Swish(z) = z sigmoid (z) 구글 브레인팀에서 만든 함수 , 다른 ReLU계열 함수보다 성능이 좋다.

*여러 활성화 함수를 사용한 결과 (앞장 조기 종료 코드에 초기화 함수만 바꿈):

ELU 함수

훈련 : 테스트 :

Leaky ReLU

훈련 : 테스트 :

Swish 함수

훈련 : 테스트 :

Batch Normalization

논란이 많은 배치정규화(나중에 더 자세히 들여다보기로 꼭) , 개념은 Deep Learning from scratch 배치 정규화 참고

구현 코드:

import numpy as np
from functools import partial
import tensorflow as tf
import mnist
import os
import time

from keras.layers import Dense
from keras.layers import BatchNormalization

import keras




def reset_graph(seed=42):
    tf.reset_default_graph()
    tf.set_random_seed(seed)
    np.random.seed(seed)
#data setting -----------------------------------
(X_train, y_train), (X_test, y_test) = mnist.load_mnist(normalize=True)

y_train = y_train.astype(np.int32)
y_test = y_test.astype(np.int32)
X_valid, X_train = X_train[:5000], X_train[5000:]
y_valid, y_train = y_train[:5000], y_train[5000:]
#------------------------------------------------


#층깊이
n_inputs = 28 * 28
n_hidden1 = 300
n_hidden2 = 100
n_outputs = 10

"""
reset_graph()


#구현1
X = tf.placeholder(tf.float32, shape=(None,n_inputs), name="X")

#연산하는 동안에는 True  아닌 동안에는 False를 반환하는 함수
training = tf.placeholder_with_default(False, shape=(), name="training")


#---------------------------------------------------
hidden1 = tf.layers.dense(X, n_hidden1, name="hidden1")
bn1 = tf.layers.batch_normalization(hidden1, training=training, momentum=0.9)
bn1_act = tf.nn.elu(bn1)

hidden2 = tf.layers.dense(bn1_act,n_hidden2, name="hidden2")
bn2 = tf.layers.batch_normalization(hidden2, training=training, momentum=0.9)
bn2_act = tf.nn.elu(bn2)

logits_before_bn = tf.layers.dense(bn2_act, n_outputs, name="outputs")
logtis = tf.layers.batch_normalization(logits_before_bn, training=training, momentum=0.9)

# ------------------------------------------------------
reset_graph()
"""

"""
#구현 2
X = tf.placeholder(tf.float32, shape=(None, n_inputs), name="X")
training = tf.placeholder_with_default(False, shape=(), name="training")


my_batch_norm_layer = partial(tf.layers.batch_normalization,
                              training=training, momentum=0.9)

hidden1 = tf.layers.dense(X, n_hidden1, name="hidden1")
bn1 = my_batch_norm_layer(hidden1)
bn1_act = tf.nn.elu(bn1)

hidden2 = tf.layers.dense(bn1_act, n_hidden2, name="hidden2")
bn2 = my_batch_norm_layer(hidden2)
bn2_act = tf.nn.elu(bn2)

logits_before_bn = tf.layers.dense(bn2_act, n_outputs, name="outputs")
logtis = my_batch_norm_layer(logits_before_bn)
"""


#구현3
#------------------------------------------------------------
reset_graph()

batch_norm_momentum = 0.9

X = tf.placeholder(tf.float32, shape=(None,n_inputs), name="X")
y = tf.placeholder(tf.int32, shape=(None), name="y")
training = tf.placeholder_with_default(False, shape=() , name="training")

with tf.name_scope("dnn"):
    he_init = tf.variance_scaling_initializer()


    my_batch_norm_layer = partial(
        tf.layers.batch_normalization,
        training=training,
        momentum=batch_norm_momentum)

    my_dense_layer = partial(
        tf.layers.dense,
        kernel_initializer=he_init)

    hidden1 = my_dense_layer(X, n_hidden1, name="hidden1")
    bn1 = tf.nn.elu(my_batch_norm_layer(hidden1))
    hidden2 = my_dense_layer(bn1, n_hidden2, name="hidden2")
    bn2 = tf.nn.elu(my_batch_norm_layer(hidden2))
    logits_before_bn = my_dense_layer(bn2, n_outputs, name="outputs")
    logits = my_batch_norm_layer(logits_before_bn)

with tf.name_scope("loss"):
    xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=logits)
    loss = tf.reduce_mean(xentropy, name="loss")


learning_rate = 0.01
with tf.name_scope("train"):
    optimizer = tf.train.GradientDescentOptimizer(learning_rate)
    training_op = optimizer.minimize(loss, name="training_op")

with tf.name_scope("eval"):
    correct = tf.nn.in_top_k(logits, y, 1)
    accuracy = tf.reduce_mean(tf.cast(correct, tf.float32), name="accuracy")


def shuffle_batch(X, y, batch_size):
    rnd_idx = np.random.permutation(len(X)) #예를들어 55000개
    n_batches = len(X) // batch_size #len(X)는 X의 행데이터 1100
    for batch_idx in np.array_split(rnd_idx, n_batches):
        X_batch, y_batch = X[batch_idx], y[batch_idx]
        yield X_batch, y_batch



init = tf.global_variables_initializer()
saver = tf.train.Saver()


n_epochs = 20
batch_size = 200


"""
extra_update_ops = tf.get_collection(tf.GraphKeys.UPDATE_OPS)

with tf.Session() as sess:
    init.run()
    start = time.time()
    for epoch in range(n_epochs):
        for X_batch, y_batch in shuffle_batch(X_train, y_train, batch_size):
            sess.run([training_op, extra_update_ops],
                     feed_dict={training: True, X: X_batch, y: y_batch})
        accuracy_val = accuracy.eval(feed_dict={X: X_valid, y: y_valid})
        print(epoch, "Validation accuracy:", accuracy_val)

    end = time.time()

    save_path = saver.save(sess, "C:\\Users\\고영민\\workspace\\parametersave\\my_batch.ckpt")
    print("걸린 시간:",round(end-start,2))


"""
with tf.Session() as sess:
    saver.restore(sess, "C:\\Users\\고영민\\workspace\\parametersave\\my_batch.ckpt")
    accuracy_val = sess.run(accuracy, feed_dict={X:X_test, y:y_test})
    print("accuracy :",accuracy_val)

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

131

132

133

134

135

136

137

138

139

140

141

142

143

144

145

146

147

148

149

150

151

152

153

154

155

156

157

158

159

160

161

162

163

164

165

166

167

168

169

170

import numpy as np

from functools import partial

import tensorflow as tf

import mnist

import os

import time

from keras.layers import Dense

from keras.layers import BatchNormalization

import keras

def reset_graph(seed=42):

tf.reset_default_graph()

tf.set_random_seed(seed)

np.random.seed(seed)

#data setting -----------------------------------

(X_train, y_train), (X_test, y_test) = mnist.load_mnist(normalize=True)

y_train = y_train.astype(np.int32)

y_test = y_test.astype(np.int32)

X_valid, X_train = X_train[:5000], X_train[5000:]

y_valid, y_train = y_train[:5000], y_train[5000:]

#------------------------------------------------

#층깊이

n_inputs = 28 * 28

n_hidden1 = 300

n_hidden2 = 100

n_outputs = 10

"""

reset_graph()

#구현1

X = tf.placeholder(tf.float32, shape=(None,n_inputs), name="X")

#연산하는 동안에는 True 아닌 동안에는 False를 반환하는 함수

training = tf.placeholder_with_default(False, shape=(), name="training")

#---------------------------------------------------

hidden1 = tf.layers.dense(X, n_hidden1, name="hidden1")

bn1 = tf.layers.batch_normalization(hidden1, training=training, momentum=0.9)

bn1_act = tf.nn.elu(bn1)

hidden2 = tf.layers.dense(bn1_act,n_hidden2, name="hidden2")

bn2 = tf.layers.batch_normalization(hidden2, training=training, momentum=0.9)

bn2_act = tf.nn.elu(bn2)

logits_before_bn = tf.layers.dense(bn2_act, n_outputs, name="outputs")

logtis = tf.layers.batch_normalization(logits_before_bn, training=training, momentum=0.9)

# ------------------------------------------------------

reset_graph()

"""

#구현 2

X = tf.placeholder(tf.float32, shape=(None, n_inputs), name="X")

training = tf.placeholder_with_default(False, shape=(), name="training")

my_batch_norm_layer = partial(tf.layers.batch_normalization,

training=training, momentum=0.9)

hidden1 = tf.layers.dense(X, n_hidden1, name="hidden1")

bn1 = my_batch_norm_layer(hidden1)

bn1_act = tf.nn.elu(bn1)

hidden2 = tf.layers.dense(bn1_act, n_hidden2, name="hidden2")

bn2 = my_batch_norm_layer(hidden2)

bn2_act = tf.nn.elu(bn2)

logits_before_bn = tf.layers.dense(bn2_act, n_outputs, name="outputs")

logtis = my_batch_norm_layer(logits_before_bn)

"""

#구현3

#------------------------------------------------------------

reset_graph()

batch_norm_momentum = 0.9

X = tf.placeholder(tf.float32, shape=(None,n_inputs), name="X")

y = tf.placeholder(tf.int32, shape=(None), name="y")

training = tf.placeholder_with_default(False, shape=() , name="training")

with tf.name_scope("dnn"):

he_init = tf.variance_scaling_initializer()

my_batch_norm_layer = partial(

tf.layers.batch_normalization,

training=training,

momentum=batch_norm_momentum)

my_dense_layer = partial(

tf.layers.dense,

kernel_initializer=he_init)

hidden1 = my_dense_layer(X, n_hidden1, name="hidden1")

bn1 = tf.nn.elu(my_batch_norm_layer(hidden1))

hidden2 = my_dense_layer(bn1, n_hidden2, name="hidden2")

bn2 = tf.nn.elu(my_batch_norm_layer(hidden2))

logits_before_bn = my_dense_layer(bn2, n_outputs, name="outputs")

logits = my_batch_norm_layer(logits_before_bn)

with tf.name_scope("loss"):

xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=logits)

loss = tf.reduce_mean(xentropy, name="loss")

learning_rate = 0.01

with tf.name_scope("train"):

optimizer = tf.train.GradientDescentOptimizer(learning_rate)

training_op = optimizer.minimize(loss, name="training_op")

with tf.name_scope("eval"):

correct = tf.nn.in_top_k(logits, y, 1)

accuracy = tf.reduce_mean(tf.cast(correct, tf.float32), name="accuracy")

def shuffle_batch(X, y, batch_size):

rnd_idx = np.random.permutation(len(X)) #예를들어 55000개

n_batches = len(X) // batch_size #len(X)는 X의 행데이터 1100

for batch_idx in np.array_split(rnd_idx, n_batches):

X_batch, y_batch = X[batch_idx], y[batch_idx]

yield X_batch, y_batch

init = tf.global_variables_initializer()

saver = tf.train.Saver()

n_epochs = 20

batch_size = 200

"""

extra_update_ops = tf.get_collection(tf.GraphKeys.UPDATE_OPS)

with tf.Session() as sess:

init.run()

start = time.time()

for epoch in range(n_epochs):

for X_batch, y_batch in shuffle_batch(X_train, y_train, batch_size):

sess.run([training_op, extra_update_ops],

feed_dict={training: True, X: X_batch, y: y_batch})

accuracy_val = accuracy.eval(feed_dict={X: X_valid, y: y_valid})

print(epoch, "Validation accuracy:", accuracy_val)

end = time.time()

save_path = saver.save(sess, "C:\\Users\\고영민\\workspace\\parametersave\\my_batch.ckpt")

print("걸린 시간:",round(end-start,2))

"""

with tf.Session() as sess:

saver.restore(sess, "C:\\Users\\고영민\\workspace\\parametersave\\my_batch.ckpt")

accuracy_val = sess.run(accuracy, feed_dict={X:X_test, y:y_test})

print("accuracy :",accuracy_val)

훈련 : 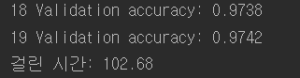테스트 :

Batch Normalization을 위의 코드와 논문의 Notation을 따라 본 정리와 내가 생각한 문제점:

잘못된 부분 수정:

*batch normalization에서 moving average 개념:

위의 코드를 보면 shuffle_batch 함수 정의에서 중복되지 않은 배열을 mini_batch shape으로 호출한다. 이는 각각의 mini_batch의 평균이 서로 독립적이다. 결국 전체 training dataset의 평균이 1 epoch을 돌린 mini_batch들의 평균의 평균과 일치한다. 문제점 : shift β 는 일치하나 scale γ 는 일치하지 않는다.

Gradient Clipping

개념만 : gradient exploding 문제를 줄이는 쉬운 방법은 역전파될 때 일정 임곗값을 넘어서지 못하게 gradient를 단순히 잘라내는 것이다.

Reusing Pretrained Layers

아주 큰 DNN을 처음부터 학습한다면 좋지 않은 방법이다. 이미 그런 비슷한 부류의 neural network가 존재하는지 보고 존재한다면 하위 층을 가져다 쓸 수 있는 좋은 방법이 있다. (직관적으로도 그러한) 이것을 transfer learning 이라한다. 이 방법은 훈련의 속도를 증가시켜줄 뿐만 아니라 필요한 훈련 데이터도 훨씬적다.

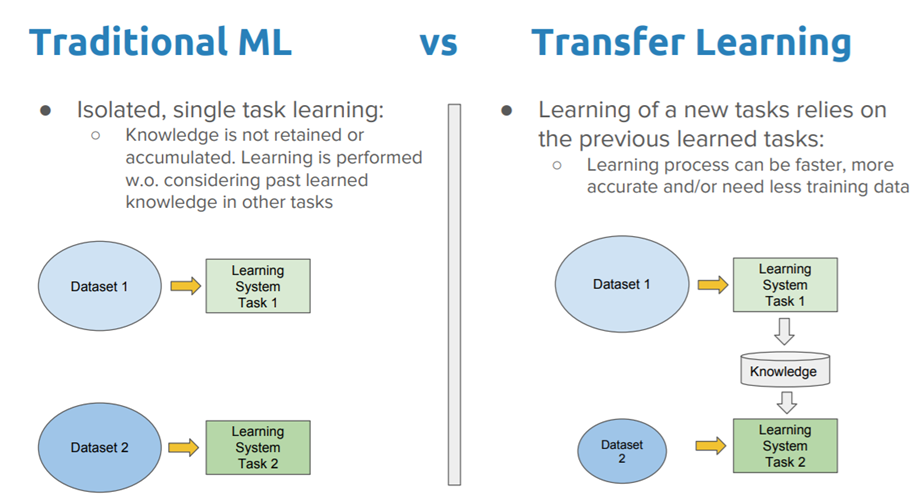
아래 코드는 위의 배치 정규화 코드를 재사용해서 구현한 코드이다.

import numpy as np
import tensorflow as tf
import mnist
def reset_graph(seed=42):
    tf.reset_default_graph()
    tf.set_random_seed(seed)
    np.random.seed(seed)

reset_graph()

saver = tf.train.import_meta_graph("C:\\Users\\고영민\\workspace\\parametersave\\my_batch.ckpt.meta")

(X_train, y_train), (X_test, y_test) = mnist.load_mnist(normalize=True)

y_train = y_train.astype(np.int32)
y_test = y_test.astype(np.int32)
X_valid, X_train = X_train[:5000], X_train[5000:]
y_valid, y_train = y_train[:5000], y_train[5000:]
#------------------------------------------------


#층깊이
n_inputs = 28 * 28
n_hidden1 = 300
n_hidden2 = 100
n_outputs = 10





for op in tf.get_default_graph().get_operations():
    print(op.name)

X = tf.get_default_graph().get_tensor_by_name("X:0")
y = tf.get_default_graph().get_tensor_by_name("y:0")

accuracy = tf.get_default_graph().get_tensor_by_name("eval/accuracy:0")

training_op = tf.get_default_graph().get_operation_by_name("train/training_op")


#또 다른 방법인 collection 추가하기
for op in (X,y,accuracy,training_op):
    tf.add_to_collection("my_important_ops",op)

X,y,accuracy,training_op = tf.get_collection("my_important_ops")





def shuffle_batch(X, y, batch_size):
    rnd_idx = np.random.permutation(len(X)) #예를들어 55000개
    n_batches = len(X) // batch_size #len(X)는 X의 행데이터 1100
    for batch_idx in np.array_split(rnd_idx, n_batches):
        X_batch, y_batch = X[batch_idx], y[batch_idx]
        yield X_batch, y_batch


n_epochs = 20
batch_size = 200
with tf.Session() as sess:
    saver.restore(sess,"C:\\Users\\고영민\\workspace\\parametersave\\my_batch.ckpt")

    for epoch in range(n_epochs):
        for X_batch, y_batch in shuffle_batch(X_train,y_train,batch_size):
            sess.run(training_op,feed_dict={X:X_batch, y:y_batch})

        accuracy_val = accuracy.eval(feed_dict={X:X_valid, y:y_valid})
        print(epoch, "Validation accuracy:", accuracy_val)

import numpy as np

import tensorflow as tf

import mnist

def reset_graph(seed=42):

tf.reset_default_graph()

tf.set_random_seed(seed)

np.random.seed(seed)

reset_graph()

saver = tf.train.import_meta_graph("C:\\Users\\고영민\\workspace\\parametersave\\my_batch.ckpt.meta")

(X_train, y_train), (X_test, y_test) = mnist.load_mnist(normalize=True)

y_train = y_train.astype(np.int32)

y_test = y_test.astype(np.int32)

X_valid, X_train = X_train[:5000], X_train[5000:]

y_valid, y_train = y_train[:5000], y_train[5000:]

#------------------------------------------------

#층깊이

n_inputs = 28 * 28

n_hidden1 = 300

n_hidden2 = 100

n_outputs = 10

for op in tf.get_default_graph().get_operations():

print(op.name)

X = tf.get_default_graph().get_tensor_by_name("X:0")

y = tf.get_default_graph().get_tensor_by_name("y:0")

accuracy = tf.get_default_graph().get_tensor_by_name("eval/accuracy:0")

training_op = tf.get_default_graph().get_operation_by_name("train/training_op")

#또 다른 방법인 collection 추가하기

for op in (X,y,accuracy,training_op):

tf.add_to_collection("my_important_ops",op)

X,y,accuracy,training_op = tf.get_collection("my_important_ops")

def shuffle_batch(X, y, batch_size):

rnd_idx = np.random.permutation(len(X)) #예를들어 55000개

n_batches = len(X) // batch_size #len(X)는 X의 행데이터 1100

for batch_idx in np.array_split(rnd_idx, n_batches):

X_batch, y_batch = X[batch_idx], y[batch_idx]

yield X_batch, y_batch

n_epochs = 20

batch_size = 200

with tf.Session() as sess:

saver.restore(sess,"C:\\Users\\고영민\\workspace\\parametersave\\my_batch.ckpt")

for epoch in range(n_epochs):

for X_batch, y_batch in shuffle_batch(X_train,y_train,batch_size):

sess.run(training_op,feed_dict={X:X_batch, y:y_batch})

accuracy_val = accuracy.eval(feed_dict={X:X_valid, y:y_valid})

print(epoch, "Validation accuracy:", accuracy_val)

코드를 보면서 name 의 활용중요성을 느낀다.

결과 :

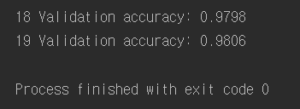
결과를 보면 알다시피 앞선 배치 정규화 때 구해놓은 변수들과 연산자들을 사용하기 때문에 시작부터 높은 정확도를 보이는 것을 볼 수 있다.

하지만 일반적으로 transfer learning을 하려하면 원래 모델의 일부만을(낮은 층) 사용하는 것이기 때문에 다른 방법이 필요하다.

다음포스팅에 이어서

11장: Deep Neural Network (p.353)

Vanishing Gradient / Exploding Gradient

Xavier 초기화, He 초기화

Batch Normalization

Gradient Clipping

Reusing Pretrained Layers

Published by gjtrj55

답글 남기기 답글 취소하기