선형대수학 – eigenvalue, eigenvector

고유값 고유벡터의 의미를 곱씹으면서 이 개념이 diagonalization theorem 에 의해 특정 행렬을 쪼갤수 있고 그렇게 쪼개진 것이 어떤 의미를 갖는지 (어떤 가정들이 필요하며, 현실적으로 어떤 제약들에 부딪히는지, 이런 것들이 어느 쪽에 응용되는지, 머신러닝에서는 어떻게 사용할 수 있을지) 등등을 생각하며 공부했다. 또한 이 개념이 확장되어 특이값 (singular value)개념이 등장하며 이는 나중에 PCA나 SVD의 핵심이 된다. 임의의 행렬을 쪼갤 수 있다는 강점은 현실에서 마주치는 문제에서 강한 힘을 발휘한다.

eigenvalue , eigenvector 의 정의 및 개념 :

서로 다른 고유값에 대응하는 고유벡터들은 일차독립이다.

기하적인 관점에서 본 고유값, 고유벡터의 의미

3차원에서 보면 $det \left | A \right |$ 는 부피와 같다. 이때 $det \left | A-\lambda I \right |$ =0은 det가 0이 되게 만드므로 해당하는 고유값이 한 개만 있을 경우 A는 면적, 2개 중복되어 있을 경우 선, 3개가 중복되면 0점에 해당한다. 하지만 이때 고유공간은 무조건 그 뺏어온 만큼의 차원을 가지는 것은 아니다. (추후에 중요한 개념)

중복도의 개념

에르미트행렬은 그냥 실수대칭행렬의 일반화다. 공부한 이유가 (실수대칭행렬은 실수인 고유값만을 가진다는 것을 보이기 위해 사용했다.)

닮음(similarity)개념

대각화정리(diagonalization theorem):

nxn 행렬 A가 일차독립인 행렬이어도 중복된 고유값에 대한 고유공간의 차원이 중복도만큼 형성되지 않을 경우 대각화할 수 없다. 즉 일차독립과고유벡터는 관련이 없다. 단 일차독립이면 n개의 0이 아닌 고유값을 가지는 것은 사실이다.

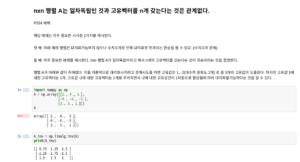
https://github.com/gjtrj55/ML/blob/master/erroreigenvalue.ipynb

중복도때문에 행렬을 대각화시킬 때 제약이 생긴다.

고유값, 고유벡터의 성질 몇가지 :

n차원 고유값은 특성방정식으로부터 구해지며 이 특성방정식은 대수학의 기본정리에 의해 복소수를 포함한 정확히 n개의 해를 갖는 것을 알고 있다. 그러므로 복소수에 대해 간략히 공부해봤다.

복소수의 기본개념 및 성질: (여기서 핵심은 복소수를 직교좌표계에 나타낼때 실수체계와는 논리적으로 엄연히 다르다는 것: 실수체에서 벡터곱은 내적인 스칼라로 표현되지만 복소수는 곱해도 복소수 그대로의 벡터형태를 지닌다.)

복소고유값, 복소고유벡터 : (회전변환이다.)

complex eigenvalue, eigenvector 그림 :

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib as mpl


A = np.array([[0.8, -0.6, 0.0],
              [0.6, 0.8, 0.0],
              [0.0, 0.0, 1.07]])

X = []
X_1 = np.array([[2.],
                [0.],
                [0.]])
for i in range(100):
    X_1 = np.dot(A,X_1)
    X.append(X_1)
X = np.array(X)
x = X[:,0,:]
x = x.reshape(-1)

y = X[:,1,:]
y = y.reshape(-1)

z = X[:,2,:]
z = z.reshape(-1)

mpl.rcParams['legend.fontsize'] = 10

fig = plt.figure()
ax = fig.gca(projection = '3d')

x = x
y = y
z = z

ax.plot(x,y,z,label = 'parametric curve')
ax.legend()

plt.show()


X = []
X_2 = np.array([[2.],
                [0.],
                [1.]])
for i in range(100):
    X_2 = np.dot(A,X_2)
    X.append(X_2)
X = np.array(X)
x = X[:,0,:]
x = x.reshape(-1)

y = X[:,1,:]
y = y.reshape(-1)

z = X[:,2,:]
z = z.reshape(-1)

mpl.rcParams['legend.fontsize'] = 10

fig = plt.figure()
ax = fig.gca(projection = '3d')

x = x
y = y
z = z

ax.plot(x,y,z,label = 'parametric curve')
ax.legend()

plt.show()

import numpy as np

import matplotlib.pyplot as plt

from mpl_toolkits.mplot3d import Axes3D

import matplotlib as mpl

A = np.array([[0.8, -0.6, 0.0],

[0.6, 0.8, 0.0],

[0.0, 0.0, 1.07]])

X = []

X_1 = np.array([[2.],

[0.],

[0.]])

for i in range(100):

X_1 = np.dot(A,X_1)

X.append(X_1)

X = np.array(X)

x = X[:,0,:]

x = x.reshape(-1)

y = X[:,1,:]

y = y.reshape(-1)

z = X[:,2,:]

z = z.reshape(-1)

mpl.rcParams['legend.fontsize'] = 10

fig = plt.figure()

ax = fig.gca(projection = '3d')

x = x

y = y

z = z

ax.plot(x,y,z,label = 'parametric curve')

ax.legend()

plt.show()

X = []

X_2 = np.array([[2.],

[0.],

[1.]])

for i in range(100):

X_2 = np.dot(A,X_2)

X.append(X_2)

X = np.array(X)

x = X[:,0,:]

x = x.reshape(-1)

y = X[:,1,:]

y = y.reshape(-1)

z = X[:,2,:]

z = z.reshape(-1)

mpl.rcParams['legend.fontsize'] = 10

fig = plt.figure()

ax = fig.gca(projection = '3d')

x = x

y = y

z = z

ax.plot(x,y,z,label = 'parametric curve')

ax.legend()

plt.show()

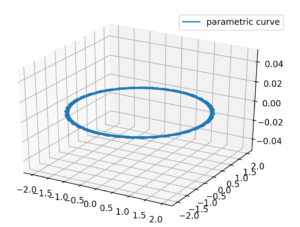복소고유값과 복소고유벡터는 회전변환이다.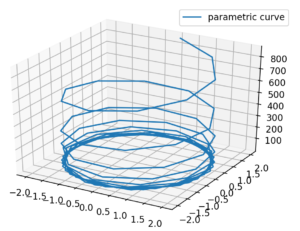

자코비 (미분행렬) , 헤시안(2차미분 행렬) 은 그냥 행렬일뿐 그 안에서 대칭행렬이거나 하는 성질들을 발견해서 고유값이 양수, 음수 등을 판별하여 극소,극대를 가지는 것을 알 수 있다.

https://github.com/gjtrj55/ML/blob/master/erroreigenvalue.ipynb

이산동적시스템은 거듭제곱(멱등)법에 대한 좋은 방법을 제시한다.

수치해석학 고유값의 반복추정 :

거듭제곱법 코드로 구현:

https://github.com/gjtrj55/ML/blob/master/sde.ipynb

선형대수학 – eigenvalue, eigenvector

Published by gjtrj55

답글 남기기 답글 취소하기