의사역행렬
Regularization 을 공부하던 중 Pseudo inverse matrix를 공부할 기회가 있어 공부했다. 선형대수학을 공부할 때 한 페이지 남짓 설명이 있던 것과 달리 매우 중요한 개념이어서 공부함에 감사한다.
애매하게 넘어갔거나 다시 상기해야 하는 내용들에 대해서 다시 공부한 뒤 진행했다.
Null space, colum space, rank 에 대해

Reduced singular value decomposition 으로 svd 를 할때 개념

의사 역행렬 정의와 성질

의사역행렬의 최소제곱문제 관계


코드 구현 :
의사역행렬 성질 중 하나인 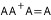
를 구현해본다. 엄밀히 하자면 고유값 행렬에서 고유값이 0이 아닌 행렬을 대각행렬로 자르고 그 수에 맞게 좌특이, 우특이 벡터를 잘라내야 하나 행렬이 작기에 무시했다.(0 * 어쩌고 = 0 이므로)
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
import numpy as np A = np.array([[1,2,3,4], [2,4,6,8], [3,6,4,8], [4,8,5,2], [5,10,3,5]]) u,s,v_T = np.linalg.svd(A) v = np.transpose(v_T) u_T = np.transpose(u) s = np.c_[s[0],s[1],s[2]] s = 1 / s s = s.reshape(3) s = np.array([[s[0], 0., 0., 0., 0.], [0., s[1], 0., 0., 0.], [0., 0., s[2], 0., 0.], [0., 0., 0., 0., 0.]]) A_ = np.dot(np.dot(v,s),u_T) print(np.dot(np.dot(A,A_),A)) print(A) |

의사역행렬을 최소제곱해와 연관한 문제를 boston housing 데이터 예제를 가지고 풀어본다. 여기서 데이터 전처리는 입력데이터에 해당하는 값만 표준화해줬으며, 나머지는 아무것도 하지 않았다. (범주로 묶거나 그런 전처리 등을 하지 않음). 이 데이터가 가역적이기 때문에 정규방정식의 해가 존재하며 , 따라서 의사역행렬로 구한 해도 정확히 같아야 한다.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
import numpy as np from keras.datasets import boston_housing (X_train, y_train),(X_test, y_test) = boston_housing.load_data() print(X_train.shape) print(y_train.shape) #표준화 작업 training dataset 만 X_train_mean = np.average(X_train, axis=0) X_train = X_train - X_train_mean #normal equation solution solution = np.linalg.inv(np.dot(np.transpose(X_train),X_train)) solution = np.dot(solution,np.transpose(X_train)) solution = np.dot(solution,y_train) print(solution) #pseudo inverse matrix u,s,v_T = np.linalg.svd(X_train) v = np.transpose(v_T) u_T = np.transpose(u) s = 1 / s s = np.diag(s) zero = np.zeros((13,391)) s = np.c_[s,zero] X_train_inv = np.dot(np.dot(v,s),u_T) solution_1 = np.dot(X_train_inv,y_train) print(solution_1) |
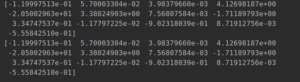
가정이 엉망이지만… 다른 곳에 의의를 둔다.
결론 :
의사역행렬은 m x n 행렬 A가 기약특이값분해를 통해 고유값행렬을 역행렬로 만들 수 있다. 이런 역행렬 비슷한 성질을 이용해 최소제곱해 문제에서 다루지 못했던 (해가 없어서, 또는 많아서) 것들을 norm 측정기준을 사용해 제일 norm이 최소화되는 답이라도 찾을 수 있게 도와준다. 이는 입력 데이터 X가 independent 하다는 가정이 없는 머신러닝 동네에서 다뤄볼 수 있는 중요한 방법 중에 하나라고 생각한다.