Ridge regression
Ridge regression의 성질에 대해 좀 더 깊게 수학적으로 들여다보자.
일반 식과 Ridge regression 식의 기대치와 분산의 차이:

|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
import numpy as np import time A = np.array([[1,7,6], [2,5,4], [3,6,2], [1,3,3]]) A = np.dot(np.transpose(A),A) Ridge = np.array([[1000,0,0], [0,1000,0], [0,0,1000]]) normal_A = np.linalg.inv(A) print(normal_A) A_result = A + Ridge A_result_inv = np.linalg.inv(A_result) print(np.round(A_result_inv,2)) #알파는 음수가 되면 안된다, Ridge = np.array([[100000,0,0], [0,100000,0], [0,0,100000]]) A_result = A + Ridge A_result_inv = np.linalg.inv(A_result) print(np.round(A_result_inv,1)) |
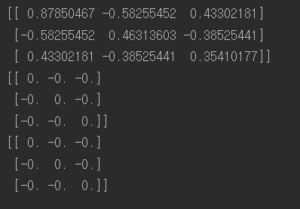
임의의 linear independent인 행렬 A를 기존 식 를 구한 것과 Ridge 규제 파라미터항
를 각각 1,000과 100,000 으로 두었을 때
를 구한 것이다. 이를 보면서 알 수 있듯이
값이 variance에 영향을 미치는데 점점 커질수록 variance를 더욱 줄이는 효과가 있다.
좀더 깔끔한 식으로 정리해본 결과 :

- Ridge E(β^) 가 biased인데 얼마나 떨어져있는지 계산할 수 있을까?
- D(data의 분산정도를 나타내는 diagonal 행렬)을 control 할 수 있는
를 구하려면 휴리스틱하게 접근해야 하는가 ?
- 변형된 notation의 가운데 term인
을 (추정식 y를 independent하다 가정을 하는 것인가?) 잘 사용하여서 biased된 것과
를 구해볼 수 있지 않을까?