11장: Deep Neural Network (p.376) (optimizer,dropout 등)

지금까지 우리는 훈련속도를 높히고 좋은 해를 찾으려고 하는 방법으로 네 가지를 알아보았다.

1. 좋은 초깃값을 적용하는 전략 ( He, Xavier 등)

2. 좋은 activation function 을 사용

3. Batch Normalization을 사용

4. pretrained network를 재사용

또 다른 속도를 높히는 방법으로 faster optimizer를 사용하는 방법이 있다. 여기서는 가장 많이 일반적으로 사용하는 optimizer 방법 몇몇개를 소개한다.

Momentum Optimization
Nesterov Accelerated Gradient
AdaGrad
RMSProp
Adam Optimization

또한 학습률 스케줄링과 overfitting을 피하기 위한 규제방법(early stopping, l1,l2 regularizer, dropout, data augmentation, max-norm regularization) 을 알아본다.

Faster Optimizers

Momentum Optimization

4장 Gradinet Descent에서도 설명했었지만 관성의 개념이 추가된 optimization이다.

momentum optimizationì ëí ì´ë¯¸ì§ ê²ìê²°ê³¼

Equation . Momentum algorithm

$1. m \leftarrow \beta m+\eta \bigtriangledown J(\Theta )$

$2. \Theta \leftarrow \Theta - m$

과거에 이동한 m을 반영하여 가중치를 업데이트하는 방식이다. β는 momentum이라하며 보통 0.9를 사용한다. 과거이동량 m에 β를 곱한 값과 gradient J(세타) 값을 더한 결과 값인 m만큼 빼주면서 업데이트한다.

기본적인 gradient descent 방법은 미분하여 기울기만큼을 학습률로 곱해서 그만큼 나아가는 것인데 만약 local minimum에 빠져있는 경우라면 기울기가 0이 되어 학습할 것이 없어진다. 즉 local minimum에 수렴하여 더이상 나아가지 않는다. 하지만 Momentum optimization은 local minimum에서의 기울기가 0이 되어서 이동량이 전혀없게 되는 경우에도 과거의 m 이동량이 있기 때문에 그만큼 학습하여 나아간다. 즉 기본적인 방식보다는 local minimum을 탈출할 수 있는 가능성이 있다는 것이다.

   optimizer = tf.train.MomentumOptimizer(learning_rate=learning_rate, momentum=0.9)
    training_op = optimizer.minimize(loss)

1 2	optimizer = tf.train.MomentumOptimizer(learning_rate=learning_rate, momentum=0.9) training_op = optimizer.minimize(loss)

Nesterov Accelerated Gradient

기본적인 momentum optimization의 변형식으로 기본 아이디어는 현재 위치가 아니라 모멘텀의 방향으로 조금 앞서서 비용 함수의 gradient를 계산하는 것이다.

$1. m\leftarrow \beta m+\eta \bigtriangledown J(\Theta -\beta m))$

$2. \Theta \leftarrow \Theta -m$

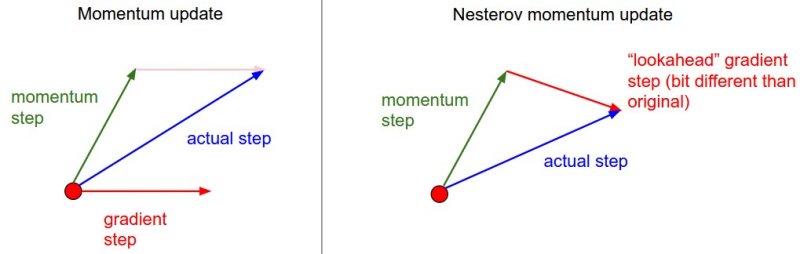
nesterov accelerated gradientì ëí ì´ë¯¸ì§ ê²ìê²°ê³¼

기본적인 momentum optimization과 달라진 점은 1. 식의 gradient부분에서 -βm 이 추가된 것 뿐이다. 이 식이 의미하는 바는 gradient를 계산하게되면 이동벡터가 gradient를 줄일 수 있는 올바른 방향을 가리키는데, 그 방향으로 조금 더 나아가서 gradient를 측정하는 것이 좀더 효율적인 움직임을 보인다는 것이다. 이런 방식들이 쌓이게 되면 기본 momentum optimization보다 훨씬 빠르게 수렴하게 도와준다. 코드의 사용은 위와 같이 간편하다.

optimizer = tf.train.MomentumOptimizer(learning_rate=learning_rate,
                                       momentum=0.9, use_nesterov=True)

1 2	optimizer = tf.train.MomentumOptimizer(learning_rate=learning_rate, momentum=0.9, use_nesterov=True)

AdaGrad

가장 가파른 차원을 따라 gradient vector의 scale을 감소시켜 문제를 해결한다.

$1. s\leftarrow s+\bigtriangledown J(\Theta )\otimes \bigtriangledown J(\Theta )$

$2. \Theta \leftarrow \Theta -\eta \bigtriangledown J(\Theta )\oslash root(s+\epsilon )$

위의 notation을 보면 벡터형식으로 $\otimes$ 원소별 곱셈을 나타낸다. 즉 $S_{i}\leftarrow S_{i}+(\frac{\partial J(\Theta )}{\partial \Theta _{i}})^{2}$ 벡터 s 의 각 원소 Si마다 구해주는 것이다. 비용함수 i번째 차원이 가파르다면 Si는 반복이 진행됨에 따라 점점 커질 것이다. 다음 식 2는 $\Theta_{i}\leftarrow \Theta _{i}-\eta (\frac{\partial J(\Theta )}{\partial \Theta _{i}}) / root(s_{i}+\epsilon )$ 을 계산하는 것과 동일하다. $root(s_{i}+\epsilon )$ term으로 나눠지기 때문에 차원별로 학습률이 다르게 감소된다. gradient가 클수록 Si도 커져 가파른 차원에서 학습률이 빠르게 감소되어 속도가 느려지고 완만한 차원에서 진행이 빨라지는 효과를 낸다. 이를 adaptive learning rate라 한다. 하지만 AdaGrad는 신경망을 훈련시킬 때 일찍 멈추는 경향이 있으므로 심층신경망에서는 사용을 하지 말아야 한다.

optimizer = tf.train.AdagradOptimizer(learning_rate=learning_rate)

1	optimizer = tf.train.AdagradOptimizer(learning_rate=learning_rate)

RMSProp

AdaGrad를 보면 과거의 gradient들이 누적되어 계산되어지는 것을 알 수 있다.(s를 보면 과거의 gradient들의 계산이 축적되는 것을 볼 수 있다.) RMSProp은 가장 최근 반복에서 비롯된 gradient만 누적함으로써 문제를 해결한다.이렇게 하기위해 첫 번째 단계에서 exponential decay를 사용한다.

$1. s\leftarrow \beta s + (1-\beta )\bigtriangledown J(\Theta )\otimes \bigtriangledown J(\Theta )$

$2. \Theta \leftarrow \Theta -\eta \bigtriangledown J(\Theta )\oslash root(s+\epsilon )$

하나의 하이퍼파라미터가 더 늘었지만 통상 감쇠율은 0.9를 사용하면 잘 맞아 떨어진다고하기에 사용한다. 이를 사용하면 1.식에서 $\bigtriangledown J(\Theta )$ 가 0.1과 곱해져 값이 작아지며 보다 작은 결과 값 s가 2식의 root에 이용된다. 이 때문에 현재 $\eta \bigtriangledown J(\Theta )$ 값이 좀더 반영될 수 있다. Adam Optimization이 나올 때까지 사랑받는 optimizer였다.

optimizer = tf.train.RMSPropOptimizer(learning_rate=learning_rate,
                                      momentum=0.9, decay=0.9, epsilon=1e-10)

1 2	optimizer = tf.train.RMSPropOptimizer(learning_rate=learning_rate, momentum=0.9, decay=0.9, epsilon=1e-10)

Adam Optimization

momentum optimization과 RMSProp과 매우 비슷한 것을 볼 수 있다.

adam optimizer formulaì ëí ì´ë¯¸ì§ ê²ìê²°ê³¼

차이나는 점은 momentum optimization에서 지수 감소합 대신 지수 감소 평균을 계산하는 것이지만 사실 이들은 상수 배인 것을 제외하면 동일하다. 보통 B1은 0.9로 B2는 0.999로 초기화하는 경우가 많다. 학습률은 0.001을 사용한다.

optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate)

1	optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate)

*이때까지 알아본 optimization은 1차 미분행렬(야코비 행렬)이다. optimization 이론에는 2차 편미분(헤시안 행렬)을 기반으로한 뛰어난 알고리즘들이 있지만 불행히도 사용이 거의 불가능하다. 왜냐면 파라미터수가 n개 라고 할때 n^2개의 2차 편미분을 계산해야하기 때문이다.

Learning Rate Scheduling

컴퓨팅 예산이 제한되어있거나 하는 경우에는 아니 일반적인 경우에 최적의 학습률을 찾고 싶을 것이다. 가장 진부한 방식으론 몇 번의 epoch만 신경망에 훈련시키고 학습곡선을 비교하여 좋은 학습률을 찾느 것이다. 이때까지 우리가 생각한 학습률은 고정되어있는 것인데 다르게 생각해볼 수 있다. 초기에 높은 학습률로 시작하고 학습속도가 느려지면 진동하지 않기 위해 낮은 학습률을 설정하여 좋은 솔루션에 도달할 수 있다. 훈련하는 동안 학습률을 감소시키는 여러가지 전략이 있으며 이를 Learning Rate Scheduling이라 하며 가장 알려진 것들을 살펴본다.

Predetermined piecewise costant learning rate:

예를들어 처음은 학습률 0.1 그리고 50epoch 후에 0.001로 바꾸는 방법이다. 이리저리 해봐야하는 단점이 있다.

Performance scheduling:

매 N step마다 (조기 종료처럼) 검증 오차를 측정하고 오차가 줄어들지 않으면 람다만큼 학습률을 감소시킨다.

Exponential scheduling:

반복 횟수 $t:\eta (t) =\eta _{0}10^{-t/r}$ 로 학습률을 설정한다. 이 방법이 잘 작동하지만 $\eta _{0}$ 와 r을 튜닝해야한다. 학습률은 매 r step마다 1/10씩 줄어들 것이다.

Avoiding Overfitting Through Regularization

규제를 통하여 과대적합을 피하는 방법에 대해 알아본다.

Early stopping

과대적합을 피하기 좋은 방법으로 코드는 따로 구현해놨다.(참고 early stopping 글) 검증 세트의 성능이 떨어지기 시작할 때 훈련을 중지시키기만 하면된다. 구현하는 한 방법은 일정한 간격으로 검증세트로 모델을 평가해서 이전의 최고 성능보다 좋으면 최고 성능의 스냅샷으로 저장하고 마지막 스냅샷이 저장된 이후 특정 step동안 바뀌지 않을 경우 중지시킨다.마지막으로 스냅샷을 복원한다.

L1, L2 Regularization

4장에서 설명하였듯이 신경망에서도 loss function에 규제를 넣어주는 방법은 동일하다. L1규제를 코드로 구현하는 방법은 ( 가중치가 W1인 하나의 hidden layer와 가중치가 W2인 출력층이 있다고 가정하자)

#가중치의 핸들을 얻는 과정
W1 = tf.get_default_graph().get_tensor_by_name("hidden1/kernel:0")
W2 = tf.get_default_graph().get_tensor_by_name("outputs/kernel:0")

#가중치의 핸들을 얻는 과정

W1 = tf.get_default_graph().get_tensor_by_name("hidden1/kernel:0")

W2 = tf.get_default_graph().get_tensor_by_name("outputs/kernel:0")

각 층에서 W1,W2 가중치의 핸들을 가져온다.

scale = 0.001 #L1 규제 하이퍼파라미터

with tf.name_scope("loss"):
    xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=logits)
    base_loss = tf.reduce_mean(xentropy, name="avg_xentropy")
    reg_losses = tf.reduce_sum(tf.abs(W1)) + tf.reduce_sum(tf.abs(W2))
    loss = tf.add(base_loss, scale * reg_losses, name="loss")

scale = 0.001 #L1 규제 하이퍼파라미터

with tf.name_scope("loss"):

xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=logits)

base_loss = tf.reduce_mean(xentropy, name="avg_xentropy")

reg_losses = tf.reduce_sum(tf.abs(W1)) + tf.reduce_sum(tf.abs(W2))

loss = tf.add(base_loss, scale * reg_losses, name="loss")

4장에서 구현하였듯이 신경망에서도 마찬가지로 L1을 구현해주면 위와 같다. 하지만 많은 층이 있다면 일일이 다써주는 것이 쉬운 일은 아니다. tensorflow는 아래와 같이 간편한 구현을 보여준다.

reset_graph()

n_inputs = 28 * 28  # MNIST
n_hidden1 = 300
n_hidden2 = 50
n_outputs = 10

X = tf.placeholder(tf.float32, shape=(None, n_inputs), name="X")
y = tf.placeholder(tf.int32, shape=(None), name="y")

scale = 0.001

my_dense_layer = partial(
    tf.layers.dense, activation=tf.nn.relu,
    kernel_regularizer=tf.contrib.layers.l1_regularizer(scale))

with tf.name_scope("dnn"):
    hidden1 = my_dense_layer(X, n_hidden1, name="hidden1")
    hidden2 = my_dense_layer(hidden1, n_hidden2, name="hidden2")
    logits = my_dense_layer(hidden2, n_outputs, activation=None,
                            name="outputs")

with tf.name_scope("loss"):                                     # not shown in the book
    xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(  # not shown
        labels=y, logits=logits)                                # not shown
    base_loss = tf.reduce_mean(xentropy, name="avg_xentropy")   # not shown
    reg_losses = tf.get_collection(tf.GraphKeys.REGULARIZATION_LOSSES)
    loss = tf.add_n([base_loss] + reg_losses, name="loss")

with tf.name_scope("eval"):
    correct = tf.nn.in_top_k(logits, y, 1)
    accuracy = tf.reduce_mean(tf.cast(correct, tf.float32), name="accuracy")

learning_rate = 0.01

with tf.name_scope("train"):
    optimizer = tf.train.GradientDescentOptimizer(learning_rate)
    training_op = optimizer.minimize(loss)

init = tf.global_variables_initializer()



n_epochs = 20
batch_size = 200

with tf.Session() as sess:
    init.run()
    for epoch in range(n_epochs):
        for X_batch, y_batch in shuffle_batch(X_train, y_train, batch_size):
            sess.run(training_op, feed_dict={X: X_batch, y: y_batch})
        accuracy_val = accuracy.eval(feed_dict={X: X_valid, y: y_valid})
        print(epoch, "Validation accuracy:", accuracy_val)

reset_graph()

n_inputs = 28 * 28 # MNIST

n_hidden1 = 300

n_hidden2 = 50

n_outputs = 10

X = tf.placeholder(tf.float32, shape=(None, n_inputs), name="X")

y = tf.placeholder(tf.int32, shape=(None), name="y")

scale = 0.001

my_dense_layer = partial(

tf.layers.dense, activation=tf.nn.relu,

kernel_regularizer=tf.contrib.layers.l1_regularizer(scale))

with tf.name_scope("dnn"):

hidden1 = my_dense_layer(X, n_hidden1, name="hidden1")

hidden2 = my_dense_layer(hidden1, n_hidden2, name="hidden2")

logits = my_dense_layer(hidden2, n_outputs, activation=None,

name="outputs")

with tf.name_scope("loss"): # not shown in the book

xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits( # not shown

labels=y, logits=logits) # not shown

base_loss = tf.reduce_mean(xentropy, name="avg_xentropy") # not shown

reg_losses = tf.get_collection(tf.GraphKeys.REGULARIZATION_LOSSES)

loss = tf.add_n([base_loss] + reg_losses, name="loss")

with tf.name_scope("eval"):

correct = tf.nn.in_top_k(logits, y, 1)

accuracy = tf.reduce_mean(tf.cast(correct, tf.float32), name="accuracy")

learning_rate = 0.01

with tf.name_scope("train"):

optimizer = tf.train.GradientDescentOptimizer(learning_rate)

training_op = optimizer.minimize(loss)

init = tf.global_variables_initializer()

n_epochs = 20

batch_size = 200

with tf.Session() as sess:

init.run()

for epoch in range(n_epochs):

for X_batch, y_batch in shuffle_batch(X_train, y_train, batch_size):

sess.run(training_op, feed_dict={X: X_batch, y: y_batch})

accuracy_val = accuracy.eval(feed_dict={X: X_valid, y: y_valid})

print(epoch, "Validation accuracy:", accuracy_val)

tf.layers.dense()에는 kernel_regularizer()라는 매개변수가 있고 이는 규제를 받을 매개변수다. 그리고 loss를 구할 때, tf.get_collection(tf.GraphKeys.REGULARIZATION_LOSSES) 로 각 가중치들의 핸들을 쉽게 얻는다.

Dropout

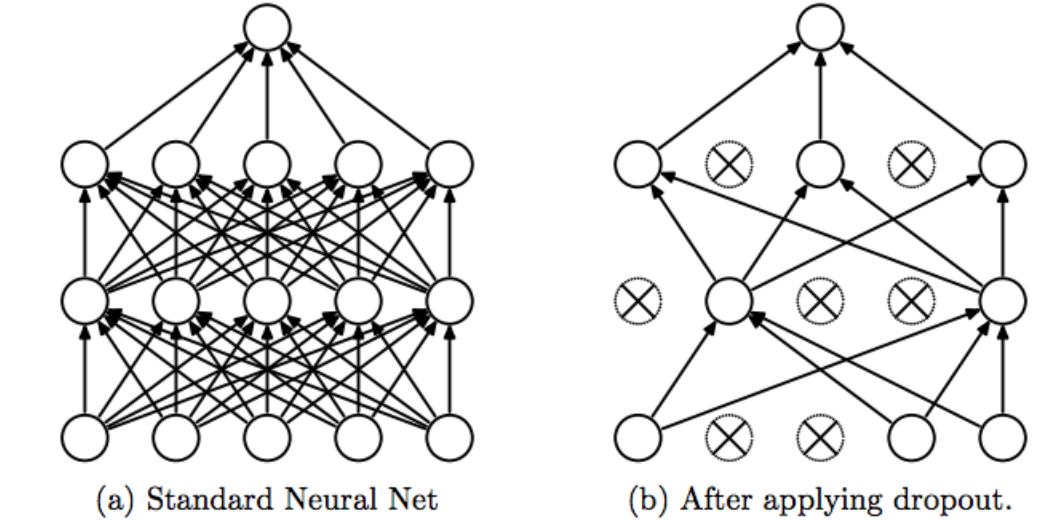
dropoutì ëí ì´ë¯¸ì§ ê²ìê²°ê³¼

그림에서 볼 수 있듯이 확률적으로 입력층의 개수를 죽이는 것이다.(보통 p = 0.5사용) 이는 각 뉴런이 0.5 확률로 dropout되게 한다. 층마다 사용하여 test할 때는 사용하지 않는다. 이때 훈련때 보다 두배 많은 입력뉴런과 연결되어 있으므로 가중치에 0.5를 곱해줘야한다. 일반적으로 (1-p) keep probability 사용

reset_graph()
n_inputs = 28 * 28  # MNIST
n_hidden1 = 300
n_hidden2 = 50
n_outputs = 10


X = tf.placeholder(tf.float32, shape=(None,n_inputs), name= "X")
y = tf.placeholder(tf.int32, shape=(None), name="y")

training = tf.placeholder_with_default(False, shape=(), name="training")

dropout_rate = 0.5
X_drop = tf.layers.dropout(X, dropout_rate, training=training)

with tf.name_scope("dnn"):
    hidden1 = tf.layers.dense(X_drop, n_hidden1, activation=tf.nn.relu,
                              name="hidden1")
    hidden1_drop = tf.layers.dropout(hidden1, dropout_rate, training=training)

    hidden2 = tf.layers.dense(hidden1_drop, n_hidden2, activation=tf.nn.relu,
                              name="hidden2")
    hidden2_drop = tf.layers.dropout(hidden2, dropout_rate, training=training)

    logits = tf.layers.dense(hidden2_drop, n_outputs, name="outputs")

with tf.name_scope("loss"):
    xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=logits)
    loss = tf.reduce_mean(xentropy, name="loss")

learning_rate= 0.01
with tf.name_scope("train"):
    optimizer = tf.train.MomentumOptimizer(learning_rate, momentum=0.9)
    training_op = optimizer.minimize(loss)

with tf.name_scope("eval"):
    correct = tf.nn.in_top_k(logits, y, 1)
    accuracy = tf.reduce_mean(tf.cast(correct, tf.float32))

init = tf.global_variables_initializer()



n_epochs = 20
batch_size = 50

with tf.Session() as sess:
    init.run()
    for epoch in range(n_epochs):
        for X_batch, y_batch in shuffle_batch(X_train, y_train, batch_size):
            sess.run(training_op, feed_dict={X: X_batch, y: y_batch, training: True})
        accuracy_val = accuracy.eval(feed_dict={X: X_valid, y: y_valid})
        print(epoch, "Validation accuracy:", accuracy_val)

reset_graph()

n_inputs = 28 * 28 # MNIST

n_hidden1 = 300

n_hidden2 = 50

n_outputs = 10

X = tf.placeholder(tf.float32, shape=(None,n_inputs), name= "X")

y = tf.placeholder(tf.int32, shape=(None), name="y")

training = tf.placeholder_with_default(False, shape=(), name="training")

dropout_rate = 0.5

X_drop = tf.layers.dropout(X, dropout_rate, training=training)

with tf.name_scope("dnn"):

hidden1 = tf.layers.dense(X_drop, n_hidden1, activation=tf.nn.relu,

name="hidden1")

hidden1_drop = tf.layers.dropout(hidden1, dropout_rate, training=training)

hidden2 = tf.layers.dense(hidden1_drop, n_hidden2, activation=tf.nn.relu,

name="hidden2")

hidden2_drop = tf.layers.dropout(hidden2, dropout_rate, training=training)

logits = tf.layers.dense(hidden2_drop, n_outputs, name="outputs")

with tf.name_scope("loss"):

xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=logits)

loss = tf.reduce_mean(xentropy, name="loss")

learning_rate= 0.01