8장: 차원축소 (p.269)
개요 :
흔한 빅데이터를 다루는 머신러닝 문제는 매우 많은 특성을 가지고 있어 훈련이 느릴 뿐아니라 좋은 솔루션을 찾기 힘들다. 하지만 불필요한 특성이 무엇인지 알아낸다면 그 특성을 제거해 조금은 가벼운 데이터셋을 만들어 낼 수 있다. 예를 들어 이미지 그림 (28 X 28) 로 이루어져 있는 MNIST 데이터셋은 숫자부분만 중요하고 나머지 배경부분의 픽셀값은 중요하지 않기 때문에 제거하면 속도가 향상된다.
차원 축소에 사용되는 주요 두가지 접근 방법
1.Projection
2.Manifold Learning
축소 기법 주요 3가지
1.PCA
2.커널 PCA
3.LLE
에 대해 공부해본다.
차원의 저주
차원이 늘어날수록 그 공간을 채워야 하는 점(데이터)의 개수가 기하급수적으로 늘어나는 것을 볼 수 있다. 이는 직관적으로 봤을 때 차원이 높아질수록 그 차원에 맞는 데이터 수가 매우 많이 필요하다는 것을 알 수 있다.
접근 방법
1.Projection
선형대수학에서 직교사영 (orthogonal projection) 개념
투영으로 기하적 관점으로 보면 예로 3차원 공간을 2차원 공간으로 즉 그림자를 그려내는 방법이다.
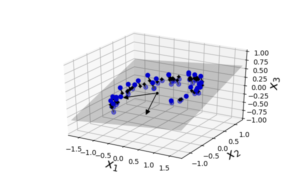
이처럼 3차원 공간에서의 시계열 형태의 데이터들을 2차원으로 projection 시키면

3차원 > 2차원 으로 데이터를 줄인 것이다. Z1 과 Z2 축은 3차원에서 그 데이터들을 가장 잘 설명해주는 두개의 축으로, 차후 뒤에서 설명하겠지만 PCA의 단점으로 뽑히는 이유이기도 하다. 왜냐면 이 새롭게 뽑힌 두 축이 무슨 특성인지 해석적으로 판단할 수 없기 때문이다. 즉 사람들이 어떤 요인에 의해 그렇게 발생했는지 설명을 할 수 없다.
다음은 projection 접근으로 해결할 수 없는 문제의 대표적인 예다.
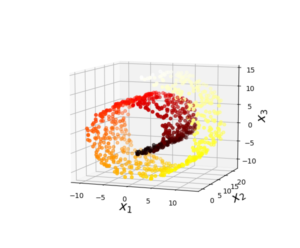
위의 스위스 롤 형태의 데이터를 투영하면 제대로 나눠지지 않고 그냥 뭉게버리는 것을 볼 수 있다.

접근방법
2.Manifold Learning
위의 스위스 롤 문제를 매니폴드 학습으로 해결할 수 있는데 결과를 보면 다음과 같다.

일반적으로 d차원 manifold 는 국부적으로 d차원 초평면으로 보일 수 있는 n차원 공간의 일부다. (d< n) 위 예시의 경우 d = 2 n = 3이다. 대부분 실제 고차원 데이터셋이 더 낮은 저차원 매니폴드에 가깝게 놓여 있다는 manifold assumption 또는 manifold hypothesis에 근거한다. (즉 고차원 데이터는 그보다 작은 차원으로 충분히 설명할 수 있다는 가정)
manifold assumption 은 종종 암묵적으로 다른 가정과 병행되곤한다. 예를 들어
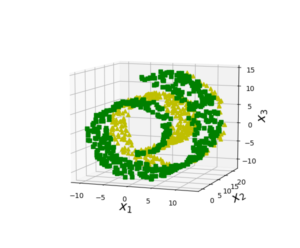
이런 데이터셋은 분류, 또는 회귀가 가능하다 가정해서 일단 매니폴드학습으로 차원을 낮춘 뒤 선형적으로 나누는 것이다.

하지만 언제나 그렇듯 항상 만능의 솔루션이 아니어서 문제점이 있다.

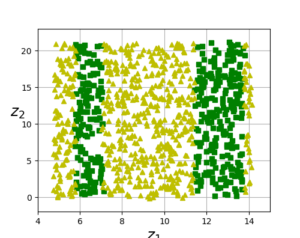
다음과 같이 꼭 좋은 솔루션이 되는 것은 아니다.
축소 기법 PCA (principal component analysis)
이론 :
주성분 분석이란 방법은 선형대수학에서 Singular Value Decomposition 즉 특이값 분해 개념을 끌고와 설명할 수 있는 개념이다. 모든 행렬은 특이값 분해로 분해 될 수 있다. 형태로 분해되며
>> 여기서는 공분산행렬

직관적인 이해 :
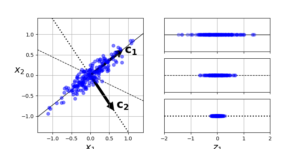
차원을 줄여 새로운 축을 만들건데 분산이 최대로 보존되는 축을 선택하는 것이 정보가 적게 손실된다. 위 그림에선 c1 축이 되겠다.
줄일 차원을 정해 축소하기:
|
1 2 |
pca = PCA(n_components = 2) X2D = pca.fit_transform(X) |
차원을 2로 줄인다.
|
1 |
print(pca.explained_variance_ratio_) |
![]()
설명된 분산의 비율을 보여주는 기능으로 앞서 보았던 (해당 고유값 / 고유값들의 합) 의 비율이다. 즉 데이터의 퍼진정도를 첫번 째 축이 84% 가량 두번 째 축이 14.6%가량 설명을 하고있다는 뜻이다.
적절한 차원의 수를 어떻게 선택하는가 ?
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
from sklearn.datasets import fetch_mldata mnist = fetch_mldata('MNIST original') from sklearn.model_selection import train_test_split X = mnist["data"] y = mnist["target"] X_train, X_test, y_train, y_test = train_test_split(X, y) pca = PCA() pca.fit(X_train) cumsum = np.cumsum(pca.explained_variance_ratio_) print(np.shape(cumsum)) d = np.argmax(cumsum >= 0.95) + 1 print(d) |
다음은 784차원( 28 x 28 ) MNIST 데이터셋을 가지고 적절한 차원수를 구해보는 예시다. 축소할 차원의 수를 임의로 정하기보다는 일반적으로 충분한 분산(95%) 이 될 때까지 더해야 할 차원 수를 선택하는 쪽을 선호한다.
cumsum 함수는 배열의 열,행 상관없이 합을 누적하여 배열에 쌓아가는 함수다. 이는 분산의 비율을 배열에 쌓아가면서 그 누적합이 0.95와 같거나 큰 값이 되는 index 값을 출력한다.
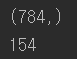
154개의 특성만으로 784차원의 분산을 95% 설명가능하다. 관점을 바꿔 더 편리하게 유지하려는 주성분의 수를 지정하기보다 보존하려는 분산의 비율을 n_components에 0~ 1 사이로 설정하는 편이 좋다.
|
1 2 3 4 |
pca = PCA(n_components=0.95) X_reduced = pca.fit_transform(X_train) print("보존비율 0.95일때 특성 수 :",pca.n_components_) print("반영한 분산 비율 :",np.sum(pca.explained_variance_ratio_)) |
![]()
압축을 위한 PCA:
|
1 2 3 |
pca = PCA(n_components = 154) X_reduced = pca.fit_transform(X_train) X_recovered = pca.inverse_transform(X_reduced) |
|
1 2 3 4 5 6 7 8 |
plt.figure(figsize=(7, 4)) plt.subplot(121) plot_digits(X_train[::2100]) plt.title("Original", fontsize=16) plt.subplot(122) plot_digits(X_recovered[::2100]) plt.title("Compressed", fontsize=16) plt.show() |
이번 코드는 데이터의 분산을 95%정도 가지고 있는 MNIST 데이터셋(특성이 약 154개) 을 반대로 변환 (inverse_ 함수)을 하여서 원 데이터와 얼마나 다른지 비교해보는 그림이다. ( 5% 자료 손실 )

점진적 PCA: (Incremental PCA )
특이값 분해 알고리즘을 실행하기 위해 전체 훈련 세트를 메모리에 올려야 한다는 것이다. 점진적 PCA (IPCA)이 개발되었다. 훈련 세트를 미니배치로 나눈 뒤 IPCA 알고리즘에 하나씩 주입한다. 이런 방식은 온라인으로 적용할 수 도 있다.
넘파이의 memmap 파이썬 클래스를 사용해 하드 디스크의 이진 파일에 저장된 매우 큰 배열을 메모리에 들어 있는 것처럼 다루는 것이다. 이 파이썬 클래스는 필요할 때 데이터를 메모리에 적재한다. IncrementalPCA는 특정 순간에 배열으 ㅣ이부만 사용하기 때문에 메모리 부족문제를 해결한다.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
from sklearn.decomposition import IncrementalPCA n_batches = 100 filename = "my_mnist.data" m, n = X_train.shape X_mm = np.memmap(filename, dtype='float32', mode='write', shape=(m, n)) X_mm[:] = X_train del X_mm X_mm = np.memmap(filename, dtype="float32", mode="readonly", shape=(m, n)) batch_size = m // n_batches inc_pca = IncrementalPCA(n_components=154, batch_size=batch_size) inc_pca.fit(X_mm) |
랜덤 PCA:
|
1 2 3 |
rnd_pca = PCA(n_components=154, svd_solver="randomized", random_state=42) X_reduced = rnd_pca.fit_transform(X_train) print(np.shape(X_reduced)) |
![]()
이 방식은 확률적인 알고리즘으로 첫 d 개의 주성분에 대한 근삿값을 빠르게 찾는다.
커널 PCA
https://yamalab.tistory.com/42
가지고 있는 차원으로 선형적으로 구분을 할 수 없을 때, 차원을 높혀서 그 차원에 매핑하여 구분할 수 있는 커널 트릭개념을 배웠웠다. 고차원 특성 공간에서의 선형 결정 경계는 원본 공간에서는 복잡한 비선형 결정경계에 해당하는 것을 배웠다. 같은 기법을 PCA에 적용해 복잡한 비선형 투영으로의 차원 축소를 가능하게 한다. 이를 커널 PCA라한다.
다음은 스위스 롤을 여러가지 kPCA를 사용하여 2차원으로 축소시킨 것이다.

원본 데이터를 그 보다 높은 차원의 공간으로 매핑한 뒤, PCA를 사용하여 투영한 것이다.
커널 선택과 하이퍼 파라미터 튜닝:
kPCA는 비지도 학습이기 때문에 좋은 커널과 하이퍼파라미터를 선택하기 위한 명확한 성능 측정 기준이 없다. 하지만 종종 지도학습의 전처리 단계로 활용되므로 그리드 탐색을 사용하여 주어진 문제에서 성능이 가장 좋은 커널과 하이퍼파라미터를 선택할 수 있다.
완전한 비지도 학습방법으로, 가장 낮은 재구성 오차를 만드는 커널과 하이퍼파라미터를 선택하는 방식도 있다.
LLE(locally linear embedding)
지역 선형 임베딩은 비선형 차원 축소 기술이다. 위의 그림과 같이 고차원의 데이터셋에 있는 데이터들이 가장 가까운 이웃에 얼마나 선형적으로 연관되어 있는지 찾은 뒤, 국부적인 관계가 가장 잘 보존되는 훈련 세트의 저차원 표현을 찾는다.
이론:
References : Hands – On Machine Learning with Scikit Learn & TensorFlow

 형태로 분해되며
형태로 분해되며 >> 여기서는 공분산행렬
>> 여기서는 공분산행렬
