6장: Decision Tree(결정 트리) (p.225)
Decision Tree
이 장에서는 결정 트리의 훈련, 시각화, 예측 방법에 대해 먼저 살펴본다. 그 후 사이킷런의 CART 훈련 알고리즘을 둘러보고 트리에 규제를 가하는 방법과 회귀 문제에 적용하는 방법을 배우도록한다. 마지막으로 결정 트리의 제약사항에 관해 이야기하며 끝을 맺겠다.
들어가기전 결정트리 수식이론 정리

결정 트리 학습과 시각화
|
1 2 3 4 5 6 |
iris = load_iris() X = iris.data[:, 2:] # petal length and width y = iris.target tree_clf = DecisionTreeClassifier(max_depth=2, random_state=42) tree_clf.fit(X, y) |
깊이가 2인 결정 트리로 root node에서 시작해 꽃잎의 길이가 2.45cm보다 짧으면 왼쪽으로 분류 (왼쪽은 자식 노드를 가지지 않은 노드 leaf node)로 class 를 setosa라고 분류했다. 2.45cm 보다 큰 꽃잎은 오른쪽으로 분류되고 꽃잎의 너비를 기준으로 다시 분류가 된다. 너비가 1.75cm보다 작으면 versicolor , 크면 virginica로 분류했다. 결정 트리의 장점으로 데이터의 전처리가 거의 필요하지 않다는 것이 있다. samples는 분류된 샘플 개수를 의미하며 value 는 분류된 샘플 개수 중에 각 label에 해당하는 개수를 나타낸다. 지니 불순도는 집합에 이질적인 것이 얼마나 섞였는 지를 측정하는 지표이다.
결정트리의 결정경계

클래스 확률 추정
한 샘플이 특정 클래스 k에 속할 확률을 추정할 수도 있다. 예를 들어 길이가 5cm, 너비가 1.5cm인 꽃잎을 발견했다고 가정하면 이에 해당하는 leaf node는 깊이 2에서 왼쪽 노드이므로 결정트리는 그에 해당하는 확률을 추정한다. 즉 iris-setosa 0% , iris-versicolor 90.7%(49/54), iris-virginica 9.3%(5/54)이다.
|
1 |
print(tree_clf.predict_proba([[5,1.5]])) |
![]()
CART 훈련 알고리즘
훈련 세트를 하나의 특성 k의 임계값 t(k)를 사용해 두 개의 서브셋으로 나눈다. 그 기준은 가장 순수한 서브셋(지니 불순도가 0에 가까운) 으로 나눌 수 있는 (k , t(k))짝을 찾는 것이다. 이 알고리즘이 최소화해야 하는 비용 함수는

서브셋을 위의 기준으로 나누는 과정을 반복하면서 max_depth를 설정한 곳까지 반복되거나 불순도를 줄이는 분할을 찾을 수 없을 때 멈추게 된다.
CART 알고리즘은 탐욕 알고리즘이다. https://ko.wikipedia.org/wiki/%ED%83%90%EC%9A%95_%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98
지니 불순도 또는 엔트로피
기본적으로 결정 트리는 지니 불순도를 사용하지만 criterion 매개변수를 entropy로 지정하여 엔트로피 불순도를 사용할 수 있다.

지니 불순도가 계산 속도에서 효율적이다. 그러나 다른 트리가 만들어지는 경우 지니 불순도가 가장 빈도 높은 클래스를 한쪽 가지로 고립시키는 경향이 있는 반면 엔트로피는 조금 더 균형 잡힌 트리를 만든다.
규제 매개변수
결정트리는 규제하지 않으면 끝에까지 나누므로 과대적합되기 쉽다. 그러므로 규제를 가해야 하는데 일반적인 경우는 max_depth로 층을 제한하는 것이 있고, 다른 방법으로는 DecisionTreeClassifier 에서는 min_samples_split(분할되기 위해 노드가 가져야 하는 최소 샘플 수),min_weight_fraction_leaf, max_leaf_nodes, max_features 등이 있다. min으로 시작하는 매개변수를 증가시키거나 max로 시작하는 매개변수를 감소시키면 모델에 규제가 커진다.
min_samples_leaf 매개 변수를 사용한 규제

회귀
결정 트리를 회귀에서도 사용이 가능하다.
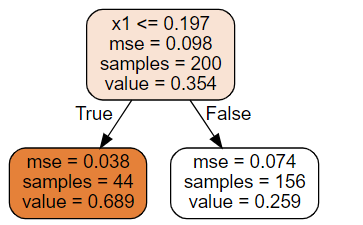
주요 차이는 각 노드에서 클래스를 예측하는 대신 어떤 값을 예측한다(연속). x1 = 0.04 이라면 value = 0.689로 분류되며 이 leaf node에 있는 44개의 샘플의 평균 타깃 값이 예측 값이 된다. 이 예측 값을 사용해 44개의 샘플에 대한 MSE를 계산하면 0.038이 된다.
두 개의 결정 트리 회귀 모델의 예측

회귀에서의 CART 알고리즘 비용함수
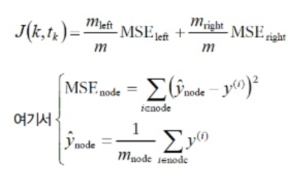
y(i)는 i번째 노드의 정답 레이블, y^(hat) node 는 y(i) 각 값들의 합에 m_node만큼 나눠준 (기대값 개념) 것이다.
결정트리 회귀 모델의 규제

불안정성
계단 모양의 결정 경계를 만들기 때문에 훈련 세트의 회전에 민감하다. 또한 훈련 데이터에 있는 작은 변화에도 매우 민감하다. 이런 불안정성을 줄이기 위해 랜덤포레스트 개념이 나오게된다.
References: Hands – On Machine Learning with Scikit – Learn & TensorFlow
