4장: 모델 훈련 part 5 (p.180)
규제가 있는 선형모델
개요:
모델의 과대적합을 감소시키는 좋은 방법은 모델을 규제하는 것이다. 다항회귀의 모델에서는 다항식의 차수를 감소시키는 것이고
선형회귀 모델에서는 보통 모델의 가중치를 제한함으로써 규제를 가한다. 이 중 대표적인 세가지 방법인 Ridge regression, Lasso regression, Elastic Net을 소개한다.
Ridge Regression
릿지회귀(또는 Tikhonov 규제)는 규제가 추가된 선형회귀 버전이다.
하이퍼파라미터 α는 모델을 얼마나 많이 규제할지 조절한다. 1/2을 곱해준 이유는 가중치 ᶿ를 미분할 때 차수가 2차여서 계산편의를 위해 넣어준 값이다. 경사하강법에 적용하려면 MSE gradient vector에 α ᶿ를 더하면 된다. 또한 ᶿ값이 1부터 시작하는데 이는 ᶿ 값이 0인 값은 bias이기 때문에 규제에서 제외한다. 결국 W를 특성의 가중치 벡터 (ᶿ 1 ~ ᶿ n)라고 정의하면 규제항은 llWll L2 norm 을 의미하기 때문에 가중치 벡터의 길이를 제한한다고 한다.
값을 최소화하기 위해 α값이 커질수록 ᶿ값이 줄어들게 된다. α가 0에 근사할수록 정규방정식처럼 unbiased but high variance를 가지고 α값이 커질수록 biased but low variance의 성질을 갖게된다.
아래 코드의 그래프의 왼쪽은 linear regression 에서 ridge α값을 (0, 10, 100)을, 오른쪽은 polynomial regression에서 ridge α값을 (0, 1e-05, 1) 을 적용한 그래프다.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 |
#규제가 있는 선형 모델 from sklearn.linear_model import Ridge np.random.seed(42) m = 20 X = 3 * np.random.rand(m, 1) y = 1 + 0.5 * X + np.random.randn(m, 1) / 1.5 X_new = np.linspace(0, 3, 100).reshape(100, 1) def plot_model(model_class, polynomial, alphas, **model_kargs): for alpha, style in zip(alphas, ("b-", "g--", "r:")): model = model_class(alpha, **model_kargs) if alpha > 0 else LinearRegression() #0이면 선형회귀사용 if polynomial: model = Pipeline([ ("poly_features", PolynomialFeatures(degree=10, include_bias=False)), ("std_scaler", StandardScaler()), ("regul_reg", model), ]) model.fit(X, y) y_new_regul = model.predict(X_new) lw = 2 if alpha > 0 else 1 plt.plot(X_new, y_new_regul, style, linewidth=lw, label=r"$\alpha = {}$".format(alpha)) plt.plot(X, y, "b.", linewidth=3) plt.legend(loc="upper left", fontsize=15) plt.xlabel("$x_1$", fontsize=18) plt.axis([0, 3, 0, 4]) plt.figure(figsize=(8,4)) plt.subplot(121) #선형회귀일때 plot_model(Ridge, polynomial=False, alphas=(0, 10, 100), random_state=42) plt.ylabel("$y$", rotation=0, fontsize=18) plt.subplot(122) #다항회귀일때 plot_model(Ridge, polynomial=True, alphas=(0, 10**-5, 1), random_state=42) plt.show() |
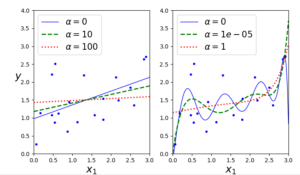
왼쪽 선형회귀 그래프를 보면 α 값이 0이면 원래 선형회귀의 그래프를, 100이면 평행한 선에 가까워 진다. 이 의미는 α값이 커질수록 규제가 커져 과대적합을 막는다.
오른쪽 다항회귀 그래프를 보면 α 값이 1일 때 0일 때의 non-linear한 선과 비교해보면 선이 직선에 가까워지는 것을 볼 수 있다. 즉 모델의 분산은 줄지만 편향은 커지게 된다.
릿지회귀를 정규방정식을 이용해 계산할 수 있는데 A는 identity matrix인데 편향에 해당하는 가중치는 규제에 포함되지 않으므로 주대각선 첫 번째 원소는 0이어야한다.
위 식을 보면 
는 대칭행렬이자 양의 정부호 행렬이므로 cholesky decomposition 에 의해 (하삼각 행렬) L 로 표현한 
행렬표현이 가능하다. 이 방법을 사용하는 이유는 컴퓨터의 연산 횟수를 많이 줄여주므로 성능이 향상된다.
다음은 sklearn에서 정규방정식을 사용한 ridge regression을 적용한 예시다.(cholesky 분해사용)
|
1 2 3 4 |
#cholesky분해를 이용한 계산 ridge_reg = Ridge(alpha=1, solver="cholesky") ridge_reg.fit(X,y) print(ridge_reg.predict([[1.5]])) |
다음은 확률적 경사 하강법을 사용했을 때다.
|
1 2 3 4 |
#SGD 를이용한 계산 sgd_reg = SGDRegressor(max_iter=5, penalty="l2") sgd_reg.fit(X,y.ravel()) print(sgd_reg.predict([[1.5]])) |
penalty 매개변수에서 l2는 SGD가 비용 함수에 가중치 벡터의 L2 norm 제곱을 2로 나눈 규제항을 추가하게 만든다. = 릿지 회귀와 같다.
Ridge regression의 규제항은 훈련하는 동안에만 비용함수에 추가된다. 모델의 훈련이 끝나면 모델의 성능을 규제가 없는 성능지표로 평가한다.
Lasso regression
Least Absolute Shrinkage and Selection Operator 회귀도 역시 선형회귀의 또 다른 규제된 버전이다.
https://bskyvision.com/193 < Lasso에 대한 직관적인 이해가 잘 설명된 사이트
Lasso는 L2 norm 대신 L1 norm을 사용한다. 이 회귀의 중요한 특징은 덜 중요한 특성의 가중치를 완전히 제거하려고 한다는 점이다.(가중치가 0이 된다.) 아래는 Lasso를 사용한 코드이다.
|
1 2 3 4 5 6 7 8 9 |
#Lasso plt.figure(figsize=(8,4)) plt.subplot(121) plot_model(Lasso, polynomial=False, alphas=(0, 0.1, 1), random_state=42) plt.ylabel("$y$", rotation=0, fontsize=18) plt.subplot(122) plot_model(Lasso, polynomial=True, alphas=(0, 10**-7, 1), tol=1, random_state=42) plt.show() |
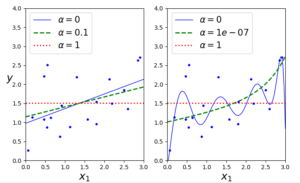
오른쪽 그래프의 α가 1e-07인 값의 선을 보면 2차방정식처럼 표현되는 선을 볼 수 있는데 이는 차수가 높은 모든 특성의 가중치가 모두 0이 되었다는 걸 알 수 있다.
Lasso는 절대값 함수라 0인 지점에서 미분 가능 점이 아니다. (좌극한과 우극한이 다르기 때문에) 하지만 subgradient vector ‘g’를 사용하면 경사 하강법을 적용하는 데 문제가 없다.
서브 그래디언트 벡터 공식 ( 추후에 따로 공부할 필요가 있음 ) 다음은 Lasso 예시코드다.
|
1 2 3 4 |
#subgradient lasso_reg = Lasso(alpha=0.1) lasso_reg.fit(X,y) print(lasso_reg.predict([[1.5]])) |
Elastic Net
Ridge 와 Lasso를 절충한 모델이다. 규제항은 이 둘을 단순히 더해서 사용하며 혼합비율인 r 을 사용해 조절한다. r = 0이면 Ridge와 같고 r = 1이면 Lasso와 같다.
사이킷런 엘라스틱넷의 간단한 예제
|
1 2 3 4 |
#elastic net elastic_net = ElasticNet(alpha=0.1, l1_ratio=0.5) elastic_net.fit(X,y) print(elastic_net.predict([[1.5]])) |
적어도 규제가 약간 있는 것이 대부분의 경우에 좋으므로 일반적으로 평범한 선형 회귀는 피해야한다. Ridge가 기본이 되지만 실제로 쓰이는 특성이 몇 개 뿐이라고 의심되면 Lasso 나 ElasticNet이 더 낫다. 특성 수가 훈련샘플 수보다 많거나 특성 몇 개가 강하게 연관되어 있을 때는 보통 Lasso가 문제를 일으키므로 Elastic Net을 선호한다.
조기 종료
규제의 색다른 방식은 검증 에러가 최솟 값에 도달하면 바로 훈련을 중단시키는 것이다. (early stopping) 아래 코드는 훈련한 것을 그래프로 그린 것이다.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 |
#조기 종료 규제 np.random.seed(42) m = 100 X = 6 * np.random.rand(m, 1) - 3 y = 2 + X + 0.5 * X**2 + np.random.randn(m, 1) #100개의 데이터셋에서 반절씩 나눔 ( 훈련 / 검증 ) X_train, X_val, y_train, y_val = train_test_split(X[:50], y[:50].ravel(), test_size=0.5, random_state=10) #다항회귀로 만든 후 표준화 시키는 파이프라인 함수 poly_scaler = Pipeline([ ("poly_features", PolynomialFeatures(degree=90, include_bias=False)), ("std_scaler", StandardScaler()), ]) #파이프라인 함수로 ( 훈련 / 검증 ) 데이터를 변환시킨 데이터 생성 X_train_poly_scaled = poly_scaler.fit_transform(X_train) X_val_poly_scaled = poly_scaler.transform(X_val) #훈련 메소드로 SGD 사용 sgd_reg = SGDRegressor(max_iter=1, tol=-np.infty, penalty=None, eta0=0.0005, warm_start=True, learning_rate="constant", random_state=42) n_epochs = 500 train_errors, val_errors = [], [] # 훈련에러, 검증에러 저장공간 for epoch in range(n_epochs): sgd_reg.fit(X_train_poly_scaled, y_train) #파이프라인변환데이터와 정답데이터 훈련 #파이프라인으로 변환된 훈련 데이터를 예측한 것 y_train_predict = sgd_reg.predict(X_train_poly_scaled) #파이프라인으로 변환된 검증 데이터를 예측한 것 y_val_predict = sgd_reg.predict(X_val_poly_scaled) #각각의 에러 값들을 저장 및 추가 train_errors.append(mean_squared_error(y_train, y_train_predict)) val_errors.append(mean_squared_error(y_val, y_val_predict)) #검증에러중에 제일 값이 작은 값의 위치 best_epoch = np.argmin(val_errors) #값이 제일 작은 검증에러의 제곱근 best_val_rmse = np.sqrt(val_errors[best_epoch]) #그래프에 화살표를 그리고 문자열을 출력하는 기능 plt.annotate('Best model', xy=(best_epoch, best_val_rmse),#화살표가 가리키는 점의 위치 xytext=(best_epoch, best_val_rmse + 1),#문자열이 출력될 위치 ha="center", arrowprops=dict(facecolor='black', shrink=0.05),#화살표의 속성 fontsize=16, ) best_val_rmse -= 0.03 # just to make the graph look better plt.plot([0, n_epochs], [best_val_rmse, best_val_rmse], "k:", linewidth=2) plt.plot(np.sqrt(val_errors), "b-", linewidth=3, label="Validation set") plt.plot(np.sqrt(train_errors), "r--", linewidth=2, label="Training set") plt.legend(loc="upper right", fontsize=14) plt.xlabel("Epoch", fontsize=14) plt.ylabel("RMSE", fontsize=14) plt.show() |
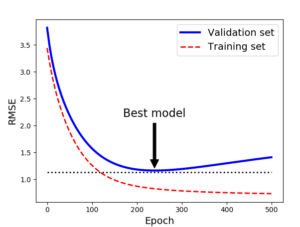
확률적 경사 하강법이나 미니배치 경사 하강법에서는 곡선이 매끄럽지 않아 최솟값에 도달했는지 어려울 수 있다. 한 가지 해결방법으로 검증 에러가 일정 시간동안 최솟값 보다 클 때 학습을 멈추고 검증 에러가 최소였을 때의 모델 파라미터로 되돌리는 것이 있다.
다음은 위의 코드를 이어받아 더 훈련시켜서 조기 종료한 코드이다.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
#조기 종료한 코드 sgd_reg = SGDRegressor(max_iter=1, tol=-np.infty, warm_start=True, penalty=None, learning_rate="constant", eta0=0.0005, random_state=42) minimum_val_error = float("inf") best_epoch = None best_model = None for epoch in range(1000): sgd_reg.fit(X_train_poly_scaled, y_train) # continues where it left off y_val_predict = sgd_reg.predict(X_val_poly_scaled) val_error = mean_squared_error(y_val, y_val_predict) if val_error < minimum_val_error: minimum_val_error = val_error best_epoch = epoch best_model = clone(sgd_reg) print("best epoch :",best_epoch) print("best model :",best_model) |
정리
이번 part에서는 선형모델이 과대적합을 감소시키는 방법으로 규제를 가하는 Ridge, Lasso, ElasticNet에 대해서 알아보았다. 이 세가지 방법은 가중치를 규제함으로써 과대적합을 피하는 것을 공부했다.
또 한가지 색다른 방법으로 조기종료에 대해 배웠다. 기본적인 아이디어는 훈련 중 더 이상 나아지지 않으면 거기서 훈련을 멈추는 것이다.
Reference : Hands- On Machine-Learning with Scikit-Learn & TensorFlow
