4장: 모델 훈련 part 4 (p.175)

학습 곡선

개요 :

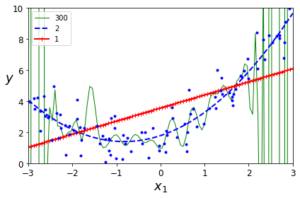
앞전 식을 300차 다항회귀 모델과 2차, 1차 선형회귀 모델로 학습했을 때의 결과다. 300차 다항회귀 모델은 과대적합되어있고 선형 회귀 모델은 과소적합되어있는 것을 볼 수 있다. 2차 모델이 적합한 것을 그림으로 쉽게 알 수 있는데 이런 모델을 어떻게 찾아낼 수 있는지를 알아본다.

얼마나 복잡한 모델을 사용할지, 어떻게 모델이 데이터에 과대적합 또는 과소 적합되었는지 알기 위한 방법으로 학습곡선을 사용한다.

하나의 방법 : 교차 검증

2장에서 모델의 일반화 성능을 추정하기 위해 교차 검증을 사용했다. 훈련 데이터에서 성능이 좋지만 교차 검증 점수가 나쁘면 모델은 과대적합된 것이고 , 만약 양쪽에 좋지 않으면 과소적합이다.

다른 방법 : 학습 곡선

아래 그래프는 훈련 세트와 검증 세트의 모델 성능을 훈련 세트 크기의 함수로 나타낸다. 이 그래프를 생성하기 위해서는 단순히 훈련세트에서 다른 서브세트를 만들어 모델을 여러번 훈련시키면 된다.

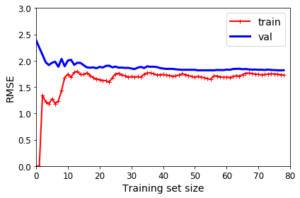
훈련데이터의 성능을 보면 데이터 사이즈가 0개 부근 일때는 샘플이 거의 없어 모델이 완벽하게 작동하는데 훈련 세트에 샘플이 추가됨에 따라 노이즈도 있고 비선형이기 때문에 모델이 훈련 데이터를 완벽히 학습하는 것이 불가능해진다. 곡선이 어느정도 평평해질 때까지 오차가 계속 상승한다. 이 위치에선 훈련 세트에 샘플이 추가되어도 평균 오차의 변화가 미미하다.

검증데이터의 성능을 보면 적은 수의 훈련 샘플로는 일반화를 제대로 할 수 없어서 오차가 크고 훈련 샘플이 많아짐에 따라 오차가 줄어든다. 하지만 선형회귀 직선은 데이터를 잘 모델링할 수 없으므로 오차의 감소가 완만해져서 훈련 세트의 그래프와 가까워진다.

위의 학습 곡선이 과소적합 모델의 전형적인 모습이다.

이 학습 곡선은 다항 회귀의 학습곡선이다. 첫 그래프와의 두가지 매우 중요한 차이점이 있다.

1.훈련 데이터의 오차가 선형 회귀 모델보다 훨씬 낮다.

2.두 곡선 사이에 공간이 있다. 이 말은 훈련 데이터에서의 모델 성능이 검증 데이터보다 훨씬 낫다는 뜻이고, 이는 과대적합 모델의 특징이다. 많은 훈련세트를 적용하면 더 가까워진다.