4장: 모델 훈련 part 3 (p.173)
다항회귀
![]() 비선형식
비선형식
가지고 있는 data가 non-linear한데도 선형 모델처럼 표현할 수 있다. 또한 학습하는 데도 선형 모델을 사용할 수 있다. 이렇게 하는 간단한 방법은 각 특성의 거듭제곱을 새로운 특성으로 추가하고 , 이 확장된 특성을 포함한 데이터 셋에 선형 모델을 훈련시키는 것이다. 이런 기법을 다항회귀 Polynomial Regression 이라한다.
예 : 간단한 2차 방정식
비선형 데이터를 노이즈를 섞어서 생성한다.
|
1 2 3 4 5 6 7 8 9 10 |
#다항 회귀 m = 100 X = 6 * np.random.randn(m,1) - 3 y = 0.5 * X**2 + X + 2 + np.random.randn(m,1) plt.plot(X, y, "b.") plt.xlabel("$x_1$", fontsize=18) plt.ylabel("$y$", rotation=0, fontsize=18) plt.axis([-10, 10, 0, 20]) plt.show() |
y = 0.5X^2 + X + 2 + random noise 인 식이다.
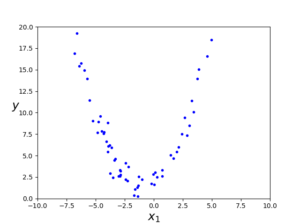
넓게 보면 이런 2차 방정식의 형태를 취하는 그래프다. 사이킷런의 PolynomialFeatures를 사용해 훈련 데이터를 변환해본다. 훈련 세트에 있는 각 특성을 제곱하여 새로운 특성으로 추가한다.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
#다항회귀 훈련 poly_features = PolynomialFeatures(degree=2, include_bias=False) X_poly = poly_features.fit_transform(X) print(X[0]) print(X_poly[0]) # X[0]의 값 제곱한 특성 추가 lin_reg = LinearRegression() lin_reg.fit(X_poly,y) print("특성추가한 절편:",lin_reg.intercept_,"\n특성추가한 기울기:",lin_reg.coef_) X_new=np.linspace(-3, 3, 100).reshape(100, 1) X_new_poly = poly_features.transform(X_new) y_new = lin_reg.predict(X_new_poly) plt.plot(X, y, "b.") plt.plot(X_new, y_new, "r-", linewidth=2, label="Predictions") plt.xlabel("$x_1$", fontsize=18) plt.ylabel("$y$", rotation=0, fontsize=18) plt.legend(loc="upper left", fontsize=14) plt.axis([-10, 10, 0, 20]) plt.show() |
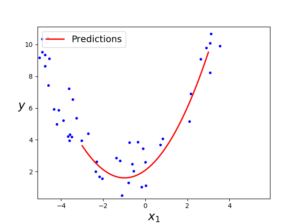
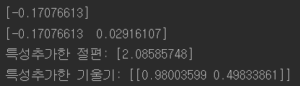
매우 비슷하게 예측한 것을 볼 수 있다.
본 식 :
예측 :
다음은 위와 같은 추정을 10번 반복한 코드이다.
|
1 2 3 4 5 6 7 8 9 10 11 |
for i in range(10): m = 100 X = 6 * np.random.randn(m, 1) - 3 y = 0.5 * X ** 2 + X + 2 + np.random.randn(m, 1) poly_features = PolynomialFeatures(degree=2, include_bias=False) X_poly = poly_features.fit_transform(X) lin_reg = LinearRegression() lin_reg.fit(X_poly,y) print("특성추가한 절편:",np.round(lin_reg.intercept_,2),"\t특성추가한 기울기:",np.round(lin_reg.coef_,2)) |

10번을 돌렸을 때 나온 절편과 기울기가 거의 차이가 없다?
이문제에 관하여 차후에 수정
이는 이 model의 noise가 ![]() 를 따르기 때문에 분산이 커봐야 1 이라는 것을 알 수 있기 때문이다.
를 따르기 때문에 분산이 커봐야 1 이라는 것을 알 수 있기 때문이다.
non-linear 한 model을 사용하면 문제가 되는 이유 :
잘못알고 있었던 것 :
다항회귀처럼 data 자체를 제곱 시키는 변환 등을 하여 변수로 추가하면, 추가된 변수는 원래의 변수로 만들어졌으므로 linear dependent하게 된다. 선형 종속은 분산 추정을 크게하여 모델의 정확도를 떨어뜨린다.
바로 잡은 것: 관점의 중요성
독립의 정의

일차 독립 ( 선형 독립 ) 정의

여기서 통계학에서의 독립과 선형 대수학의 선형 독립의 정의를 잘 생각하고 ( 둘은 서로 다르며 선형대수학에서는 독립을 정의하지 않았다. ) 머신러닝에서는 이런 두가지 관점이 섞여서 들어오기 때문에 잘 구분하여 바라보는 시각을 길러야한다. 위의 잘 못 알고 있었던 부분을 보자면 다 맞는 얘기인데 관점이 다르다는 것이다. 머신러닝 다항회귀 모델에서는 β(가중치) 관점으로 바라봤기 때문에 β가 선형독립인지만 확인하면 된다. data (x)들의 관점이 아니다.(흔히 선형대수학에서는 이들의 관점에서 얘기한다.)
결국 10번을 돌렸을 때 분산이 커서 값들이 이리 저리 튈거라(data들이 선형종속이 되니까) 생각한 내 예상과는 다르게 β 관점에서 기술한 것이기 때문에 표준편차가 1인 분포를 따라 안정적으로 나온 것이다.