4장: 모델 훈련 part 1 (p.155)
개요 : 이 장에서는 머신러닝 모델과 훈련 알고리즘을 들여다 보는 chapter이다. 이 장의 주요 part는 다음과 같다.
1.Linear Regression
2.Gradient Descent
3.Polynomial Regression
4.Learning Curve
5.규제가 있는 Linear model
6.Logistic Regression
Part 1 .Linear Regression
선형회귀는 다른 포스팅에서 다룬 적이 있으니 생략하고 코드 구현 중심으로 설명한다. (밑의 식이 성립하기 위해서는 선형적으로 독립이어야 한다.)
위와 같은 OLS 추정, 즉 명시적인 해를 구현해보기 위한 코드를 작성해 본다.
|
1 2 3 4 5 6 7 8 9 |
# Linear Regression X = 2 * np.random.rand(100,1) y = 4 + 3 * X + np.random.randn(100,1) plt.plot(X, y, "b.") plt.xlabel("$x_1$", fontsize=18) plt.ylabel("$y$", rotation=0, fontsize=18) plt.axis([0, 2, 0, 15]) plt.show() |
X (100,1) 형태의 행렬이고 y도 역시 (100,1) 행렬이다. 관계식은 linear regression인 y = 4 + 3X + 𝜀 이며 위 식의 X,y와의 관계를 그래프로 나타내면 다음과 같다.
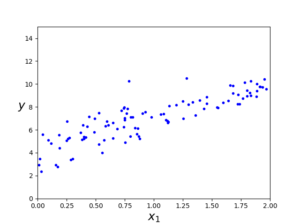
이제 정규방정식을 사용해 b를 계산해본다.
|
1 2 3 4 5 |
#명시적인해 구하기 X_b = np.c_[np.ones((100,1)),X] #모든 샘플에 X0 = 1을 추가 theta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y) print(theta_best) |
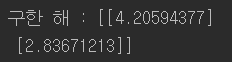
관계식의 해는 (4,3) 인데 대충 비슷하게 찾았다. 이제 구한 해를 가지고 예측을 해보면 다음과 같다.
|
1 2 3 4 5 6 7 8 9 10 11 |
#구한 해로 예측 X_new = np.array([[0],[2]]) X_new_b = np.c_[np.ones((2,1)),X_new] y_predict = X_new_b.dot(theta_best) print("예측 값 :",y_predict) print("실제 값 :",4,"\n\t",10) plt.plot(X_new, y_predict, "r-") plt.plot(X, y, "b.") plt.axis([0,2,0,15]) plt.show() |
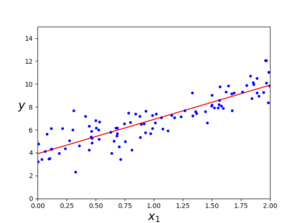
같은 작업을 하는 사이킷런 코드 :
|
1 2 3 4 5 |
#sklearn code lin_reg = LinearRegression() lin_reg.fit(X,y) print("절편:",lin_reg.intercept_,"\n기울기:",lin_reg.coef_) print("예측 :",lin_reg.predict(X_new)) |
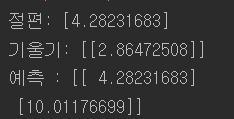
계산복잡도 문제:
절편을 포함한 특성 수는 (N+1)개인데 
= (N+1) x (N+1) 크기가 되는 역행렬을 계산한다. 역행렬을 계산하는 계산복잡도(computational complexity)는 특성 수가 늘어날 수록 기하급수적으로 증가한다. 다행인 것은 훈련 세트의 샘플 수에는 선형적으로 증가한다. 그러므로 메모리 공간이 허락된다면 큰 훈련 세트도 효율적으로 처리할 수 있다. 또한 학습된 선형 회귀 모델은 예측이 매우 빠르다. 예측 계산 복잡도는 샘슬 수와 특성 수에 선형적이다.
정리 :
정규방정식으로 linear regression의 해를 구할 때 inverse matrix를 구하는 과정에서의 계산복잡도는 특성수에 따라 기하급수적으로 증가해 문제가 있지만 샘플 수에는 선형적이어서 별 영향을 끼치지 않는다. 이후 구해진 해를 가지고 예측을 할 때는 (예측 계산 복잡도) 선형적이어서 매우 빠르다.
