2장: 머신러닝프로젝트 처음부터 끝까지 (p.90)
이전 내용 : 캘리포니아 주택 가격 dataset을 사용하여 캘리포니아의 주택 가격 모델을 만드는 연구를 진행하는 상황을 가정했다. 간단한 데이터의 구조를 살펴보았고, 계층적 샘플링과 무작위 샘플링에 대해서 살펴보았다.
1.데이터 이해를 위한 탐색과 시각화
복사본을 만들어 보호한다.
|
1 |
housing = strat_train_set.copy() |
지리적 데이터 시각화

앞서 우리는 dataset의 key에 latitude(위도)와 longitude(경도) 라는 지리적 정보가 포함되어 있어 지리적으로 시각화 해볼 수 있다. (discrete하게)
|
1 2 3 4 |
housing.plot(kind="scatter", x="longitude", y="latitude") plt.xlabel('경도', fontproperties=fontprop) plt.ylabel('위도', fontproperties=fontprop) plt.show() |
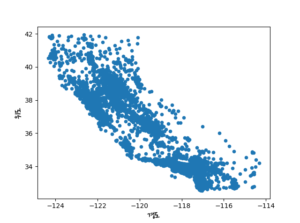
어떤 특별 패턴을 찾기 힘드므로 alpha = 0.1로 주면 데이터가 밀집된 영역을 잘 보여준다.
|
1 |
housing.plot(kind="scatter", x="longitude", y="latitude", alpha=0.1) |

더 두드러진 패턴을 보기위해 매개변수를 다양하게 조절해본다.
|
1 2 3 |
housing.plot(kind="scatter", x="longitude", y="latitude", alpha=0.4, s=housing["population"]/100, label="population", figsize=(10,7), c="median_house_value", cmap=plt.get_cmap("jet"), colorbar=True, sharex=False) |
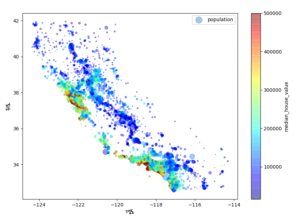
주택가격은 지역과 인구밀도에 관련이 매우 크다는 걸 알 수 있다.
상관관계 조사
standard correlation coefficient (피어슨 상관계수) 를 이용하여 중간 주택 가격이 다른 특성들과 어떤 관계가 있는지를 -1 (강한 음의 관계) 에서 1 (강한 양의 관계) 로 알려준다.
|
1 2 3 |
#상관계수조사 corr_matrix = housing.corr() print(corr_matrix["median_house_value"].sort_values(ascending=False)) |

median_income(중간 소득)이 중간 주택가격에 영향을 상대적을 많이 끼치는 것을 알 수 있다. 또한 latitude(위도)를 보면 약한 음의 상관관계(-0.14)임을 보이는데 이는 북쪽으로 갈수록 가격이 조금씩 내려가는 경향이 있다.)
주의사항 : 상관계수는 선형적인 상관관계만 나타내기 때문에 non-linear한 관계는 파악할 수 없다 ( ex: x가 0에 가까워지면 y가 증가한다.) 마지막 줄에 있는 그림들은 두 축이 independent 하지 않음에도 상관계수가 0이다(non-linear 한 예시) . 한가지 더 상관계수는 기울기와 상관없다.
또 다른 방법은 판다스에 scatter_matrix 함수를 사용하여 각각의 숫자형 특성이 다른 특성들과 어떤 관계가 있는지 보여주는 방법이 있다. 하지만 이 dataset은 특성이 11개여서 121개 그래프가 나오니 몇 가지만 그려보기로 한다.
|
1 2 3 4 |
#각각 특성 그려보기 attributes = ["median_house_value", "median_income", "total_rooms", "housing_median_age"] scatter_matrix(housing[attributes], figsize=(12,8)) plt.show() |

대각선은 자기 자신 특성이다. 아까 알아보았듯이 주간 주택 가격에 중간 소득이 영향을 많이 미치므로 그 부분만 확대해서 보기로 한다.
|
1 2 3 4 |
housing.plot(kind="scatter", x="median_income", y="median_house_value", alpha=0.1) plt.xlabel('중간소득', fontproperties=fontprop) plt.ylabel('중간주택가격', fontproperties=fontprop) plt.show() |
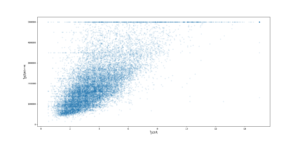
특징 1. 상관관계가 강하다.
2. 50만 가격대와 35만 가격대 등이 수평선 형태다. 알고리즘이 이런 이상한 형태를 학습하지 않도록 해당 구역을 제거하는 것이 좋다.
특성 조합으로 실험
특성들을 조합해봄으로써 유용한 관계를 찾을 수 있다. 예를 들어 특정 구역의 방 개수는 얼마나 많은 가구수가 있는지 모른다면 그다지 유용하지 않다. 가구당 방의 개수가 중요하기 때문에 이런 특성들을 만들어본다.
|
1 2 3 4 5 6 7 |
#특성조합 housing["rooms_per_household"] = housing["total_rooms"] / housing["households"] housing["bedrooms_per_room"] = housing["total_bedrooms"] / housing["total_rooms"] housing["population_per_household"] = housing["population"] / housing["households"] corr_matrix = housing.corr() print(corr_matrix["median_house_value"].sort_values(ascending=False)) |

새로운 bedrooms_per_room 특성은 전체 방개수(0.13) 이나 침대 개수(0.04) 보다 상관관계가 훨씬 높다.
전체 코드 :
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 |
from zlib import crc32 import matplotlib.font_manager as fm font_path ='C:\Windows\\Fonts\\NanumPen.ttf' fontprop = fm.FontProperties(fname=font_path, size=18) from sklearn.model_selection import train_test_split import os import tarfile from six.moves import urllib import pandas as pd import csv import matplotlib.pyplot as plt import numpy as np from sklearn.model_selection import StratifiedShuffleSplit from pandas.plotting import scatter_matrix #데이터 읽어들이기 # df = pd.read_csv('housing.csv',names=['longitude','latitude','housing_median_age','total_rooms', # 'total_bedrooms','population','households','median_income', # 'median_house_value','ocean_proximity']) housing = pd.read_csv('housing.csv') #복사본 만들기 housing = strat_train_set.copy() #지리적 데이터 시각화 #housing.plot(kind="scatter", x="longitude", y="latitude", alpha=0.4, # s=housing["population"]/100, label="population", figsize=(10,7), # c="median_house_value", cmap=plt.get_cmap("jet"), colorbar=True, sharex=False) #plt.xlabel('경도', fontproperties=fontprop) #plt.ylabel('위도', fontproperties=fontprop) #plt.show() #상관계수조사 #corr_matrix = housing.corr() #print(corr_matrix["median_house_value"].sort_values(ascending=False)) #각각 특성 그려보기 #attributes = ["median_house_value", "median_income", "total_rooms", "housing_median_age"] #scatter_matrix(housing[attributes], figsize=(12,8)) #중간소득으로 중간주택가격 비교그래프 #housing.plot(kind="scatter", x="median_income", y="median_house_value", alpha=0.1) #plt.xlabel('중간소득', fontproperties=fontprop) #plt.ylabel('중간주택가격', fontproperties=fontprop) #plt.show() #특성조합 housing["rooms_per_household"] = housing["total_rooms"] / housing["households"] housing["bedrooms_per_room"] = housing["total_bedrooms"] / housing["total_rooms"] housing["population_per_household"] = housing["population"] / housing["households"] corr_matrix = housing.corr() print(corr_matrix["median_house_value"].sort_values(ascending=False)) |
References : Hands-On Machine Learning with Scikit-Learn & TensorFlow
