배치정규화 (batch normalization)
앞전에서 가중치의 초기 값을 어떻게 주느냐에 따라서 결과가 달라지는 것을 보았다. 이는 적절한 가중치를 줌으로써 data의 분포가 골고루 분포되게 하는 것이 핵심이다. 초기값에 따라 결과가 좌지우지되는 위험을 줄이고자 나온 방법에 대해 공부해 보았다.
Batch Normalization이란?

그림에선 활성화 함수 앞에 있지만, 뒤에 쓸수도 있다. (이 부분에도 논쟁이 많음)
Neural Network에서 대표적인 문제점으로 gradient vanishing, exploding gradient, internal covariance shift 라는 문제가 있다. batch normalization은 이런 문제점을 직접적으로 해결하는 방법 중 하나다.
문제점 : Internal Covariance Shift 현상이란?
Network의 각 층이나 Activation마다 input 의 distribution이 달라지는 현상이다. 이게 무슨 말이냐면
학습 시 해당 Layer는 해당 Layer의 전의 모든 Layer의 parameter 변화에 영향을 받게되며 깊이 (층)이 깊어질수록 이전 Layer parameter의 작은 변화가 증폭되어( 이 부분이 이해가 안감.) 이후에 위치한 Layer의 parameter의 추정치에 큰 영향을 미칠 수 있음. 이처럼 학습하는 도중에 이전 Layer parameter의 변화로 인해 현재 Layer의 입력분포가 바뀌는 현상을 covariate shift 라 한다. 라고 함.
Solution
whitening 이라는 전처리 기법이 있는데 이는 input의 feature 들을 uncorrelated 하게 만들어주고 input feature 각각의 variance 를 1로 만들어주는 작업이다. 하지만 이는 공분산 행렬 계산, 역행렬 계산 등 계산이 많아 문제가되며, 또한 normalization을 (whitening 작업) 할 때, 일부 parameter들의 영향이 무시되는 문제가 발생한다. 예를 들어 input 값이 ax + b 일경우 E[ax + b] (기대치) 에서 빼주는 과정에서 b가 상쇄되어 b의 영향이 없어진다. 분산일 경우 그 영향은 더욱 악화된다.
그래서 등장한 것이 Batch Normalization 이다.
batch normalization은 몇 가지 가정을 한 뒤 시작한다. 그 조건은 (논문 발췌)
- 각각의 feature들이 이미 uncorrelated 되어있다고 가정하고, feature 각각에 대해서만 scalar 형태로 mean과 variance를 구하고 각각 normalize 한다.
- 단순히 mean과 variance를 0, 1로 고정시키는 것은 오히려 Activation function의 nonlinearity를 없앨 수 있다. 예를 들어 sigmoid activation의 입력이 평균 0, 분산 1이라면 출력 부분은 곡선보다는 직선 형태에 가까울 것이다. 또한, feature가 uncorrelated 되어있다는 가정에 의해 네트워크가 표현할 수 있는 것이 제한될 수 있다. 이 점들을 보완하기 위해, normalize된 값들에 scale factor (gamma)와 shift factor (beta)를 더해주고 이 변수들을 back-prop 과정에서 같이 train 시켜준다.
- training data 전체에 대해 mean과 variance를 구하는 것이 아니라, mini-batch 단위로 접근하여 계산한다. 현재 택한 mini-batch 안에서만 mean과 variance를 구해서, 이 값을 이용해서 normalize 한다.
수식의 표현은 다음과 같다.

수식을 들여다보면 mini-batch B = {x1…m} 이라는 m개의 input data의 집합에 대해 mean 과 variance를 구한 것이다. variance 부분에 ε은 코딩할 때 0으로 나누는 사태를 방지하고자 넣은 것.
설명 : 통계학에서 표준화 (standardization) 개념

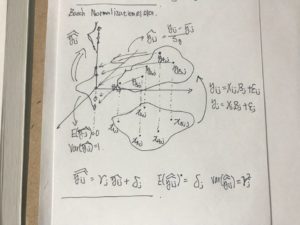
위의 수식을 좌표로 표현하면 다음과 같다. ( 교수님께 들은 얘기 참고)
‘Training 할 때는 mini-batch의 평균과 분산으로 normalize 하고, Test 할 때는 계산해놓은 이동 평균으로 normalize 한다. Normalize 한 이후에는 scale factor와 shift factor를 이용하여 새로운 값을 만들고, 이 값을 내놓는다. 이 Scale factor와 Shift factor는 다른 레이어에서 weight를 학습하듯이 back-prop에서 학습하면 된다.’ 라는 흐름이다. – 라고 쓰여 있다. (블로그 참고 )
코드 참고
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 |
class BatchNormalization: """ http://arxiv.org/abs/1502.03167 """ def __init__(self, gamma, beta, momentum=0.9, running_mean=None, running_var=None): self.gamma = gamma self.beta = beta self.momentum = momentum self.input_shape = None # 합성곱 계층은 4차원, 완전연결 계층은 2차원 # 시험할 때 사용할 평균과 분산 self.running_mean = running_mean self.running_var = running_var # backward 시에 사용할 중간 데이터 self.batch_size = None self.xc = None self.std = None self.dgamma = None self.dbeta = None def forward(self, x, train_flg=True): self.input_shape = x.shape if x.ndim != 2: N, C, H, W = x.shape x = x.reshape(N, -1) out = self.__forward(x, train_flg) return out.reshape(*self.input_shape) def __forward(self, x, train_flg): if self.running_mean is None: N, D = x.shape self.running_mean = np.zeros(D) self.running_var = np.zeros(D) if train_flg: mu = x.mean(axis=0) xc = x - mu var = np.mean(xc ** 2, axis=0) std = np.sqrt(var + 10e-7) xn = xc / std self.batch_size = x.shape[0] self.xc = xc self.xn = xn self.std = std self.running_mean = self.momentum * self.running_mean + (1 - self.momentum) * mu self.running_var = self.momentum * self.running_var + (1 - self.momentum) * var else: xc = x - self.running_mean xn = xc / ((np.sqrt(self.running_var + 10e-7))) out = self.gamma * xn + self.beta return out def backward(self, dout): if dout.ndim != 2: N, C, H, W = dout.shape dout = dout.reshape(N, -1) dx = self.__backward(dout) dx = dx.reshape(*self.input_shape) return dx def __backward(self, dout): dbeta = dout.sum(axis=0) dgamma = np.sum(self.xn * dout, axis=0) dxn = self.gamma * dout dxc = dxn / self.std dstd = -np.sum((dxn * self.xc) / (self.std * self.std), axis=0) dvar = 0.5 * dstd / self.std dxc += (2.0 / self.batch_size) * self.xc * dvar dmu = np.sum(dxc, axis=0) dx = dxc - dmu / self.batch_size self.dgamma = dgamma self.dbeta = dbeta return dx |
코드 해석은 나중에… (난해함)
나중에 더 깊이 공부할 때 다루기로
참고 – https://shuuki4.wordpress.com/2016/01/13/batch-normalization-%EC%84%A4%EB%AA%85-%EB%B0%8F-%EA%B5%AC%ED%98%84/