M.L (p.207)

ReLU function을 사용할 때의 초깃값

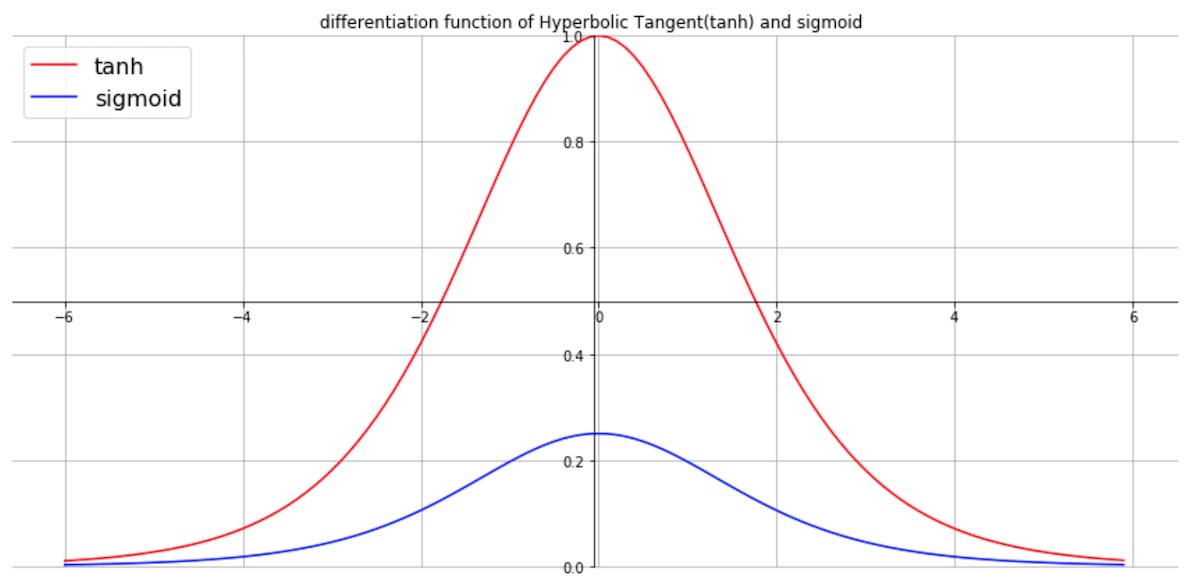
앞서 본 것처럼 Xavier 초깃값은 sigmoid, tanh 같은 activation function의 미분(기울기)가 높은 구간 주변 , 즉 대칭을 이루는 중앙 부분에  넓게 data를 적절히 분포해야 학습을 잘 할수 있다는 것을 알았다.

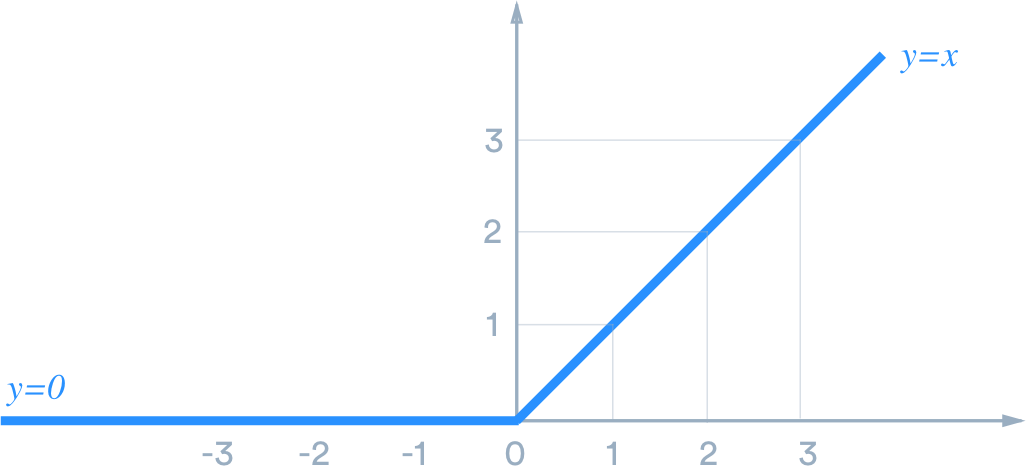
ReLU는  밑에 처럼 0보다 작으면 0을  0보다 크면 자기 자신을 출력하는 function이다.

이를 미분하면 기울기는

0보다 큰 상태에서는 기울기가 1인 상태가 된다. 즉 가운데를 중심으로 대칭인 위의 다른 function들과는 다르다. 책에서 ReLU는 음의 영역이 0이라서 data를 더 넓게 분포시키기위해 표준편차가 루트 ( 2/ n ) 인 정규분포를 사용한다고 한다. ( 내 생각으론 넓게 분포시키는 것보다 data를 오른쪽으로 shift 하면 더 잘맞지 않을까 생각)

무튼 사용의 결과를 보면 이렇다.

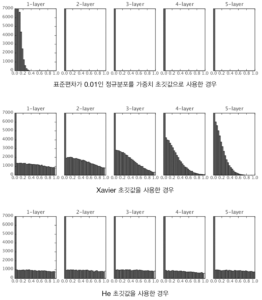
ReLU를 사용할 때는 He 초깃값을, sigmoid 같은 s자 ( 기울기 대칭 ) 은 Xavier 초깃값을 쓰는 것이 현재의 모범사례라고 한다. (이 책 년도 기준)

MNIST 데이터셋으로 본 가중치 초깃 값 비교

층별 뉴런수가 100개인 5층 신경망에서 활성화 함수로 ReLU를 사용

가중치의 초깃값은 신경망 학습에서 아주 중요한 포인트이다.