Neural Network에 대한 내 정리
개요 ( 생각열기 ) : 머신러닝은 어떻게 오게된 것인가?
 linear regression
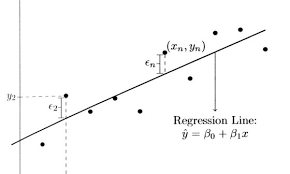
linear regression
통계학적으로 접근해보자면 우리는 어떤 현상들이라던지, 문제들에 대해 예측을 하고 싶어한다. 예를 들어 위의 linear regression이 공부시간(x)에 관한 성적(y) 라고 한다면, 다음에 기대하는 성적에 대해 알기 위해서는 전적으로 과거의 데이터에 의존해야한다. 과거의 데이터를 가지고 예측을 할 수 있는 어떠한 model(function)을 만든다면 그 model이 그 현상을 잘 설명할 때( 예측) 좋은 성과를 거둔다.
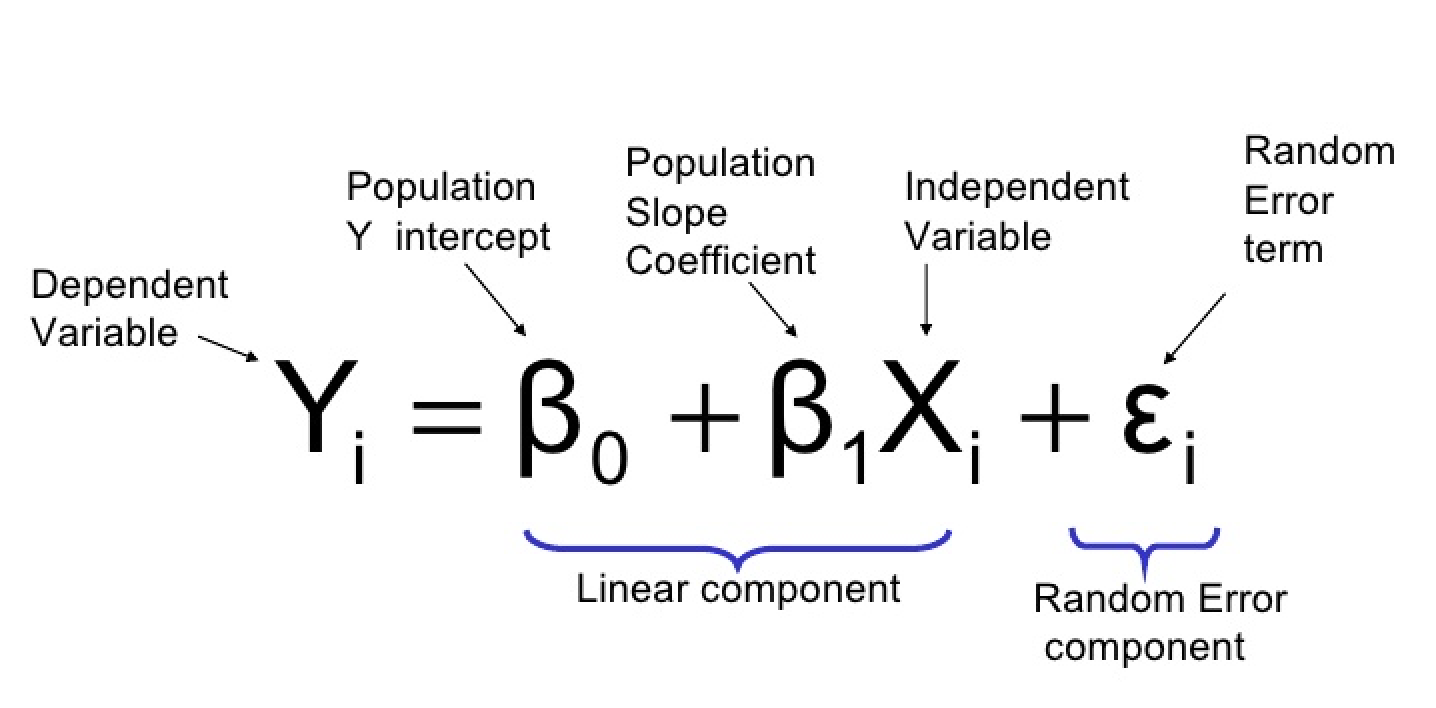
간단히 말하면 data들은 위의 그래프로 보면 산포해있고 이를 가장 잘 설명해주는 선 하나를 찾는 것이 목표가 될 것이다. 다르게 접근하자면 모든 데이터는 하나의 선으로 완벽하게 표현할 수 있는데 우리가 설명할 수 없는 요인에 의하여 직선 위에서 벗어난 것으로 보는 것이다. 따라서 위의 식처럼 종속변수 Y는 bias와 독립 변수 X 그리고 설명되지 않는 오차 ε 의 합으로 나타낼 수 있다. 즉 random variable ε이 존재하여 (그림)linear component 부분이 관측된 data로 확실하게 주어져도 Yi 값을 정확하게 맞추는 것이 어렵게 된다. 즉 확률적으로 움직이게 된다.
확률적으로 움직이게 되면 distribution이 형성되고 이 distribution을 잘 설명해주는 model이 필요한 것이다. (위의 맥락과 같음)
만약 linear model이 맞는 모델이 아니라면
(이 부분은 나중에 hands on machine learning을 집중적으로 공부할 때 설명)
- equation의 차수를 높힌다. <- Non-linear한 model로 접근 ( 추정해야할 parameter 수 급격히 증가
- 차원을 높힌다. <- 차원의 저주 문제 발생
- Activation function은 monotone increasing function 의 특성을 가지며, 거리를 벌리는 ? 역할
이런 문제를 다루기 쉽지 않기 때문에 Machine Learning은 비교적 다루기 쉬운 Linear Model에 Activation function을 결합하는 결론에 도달한다.
1. Flow of Network

Fully connected neural network 의 기본적인 흐름으로써 잘 나타내주는 그림( MNIST데이터셋 그림) 이다.
Affine transformation (linear combination ) 후에 변환된 데이터를 activation function으로 non – linear하게 만드는 작업을 거친다. 이 과정을 되풀이(hidden layer를 쌓는 과정)한다. 후에 마지막으로 정답 데이터(label data)와 비교하여 값 또는 정확도를 산출한다.
2. Affine transformation
가령, 우리에게 주어진 data가 어떤 한 병원에서 암 진단여부를 기록한 환자들의 dataset 이라 해보자. ( 이해를 위한 예시이므로 독립성검정, 변수의 해석 등은 무시한다.)
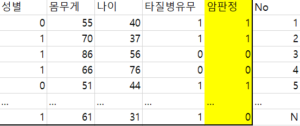 넘겨받은 환자의 데이터수는 N개
넘겨받은 환자의 데이터수는 N개
환자의 변수 목록으로 성별 몸무게 나이 타질병유무 4개의 변수를 담은 데이터 (N,4)를 input data라 하고 암판정만을 따로 담은 정답데이터를 (N,1) 형태의 label data라 하자.

input data를 affine transformation을 통해, 예를 들어 (N,4) input data를 (4, 1) weight를 행렬곱하여 (N,1)의 data로 변환할 수 있으며 label data 의 형태와 맞게 변환시킬 수 있다. ( matrix의 shape이 같아야만 오차를 계산하는데 있어 유용하기 때문에 이 작업을 수행)
3. Activation function
affine transformation을 통해 우리는 label data와 input data의 형태가 같게 만든 것을 볼 수 있다.
(여기서 풀리지 않은 궁금증 : affine transformation과 activation function을 반복하여 수행할 때, 층을 여러개 두는 이유)
Activation function을 통해 non- linear하게 만들어 준후 (책에서 이 과정이 필요한 이유는 non-linear한 function(Affine transformation)을 사용하지 않으면 hidden layer가 많든 적든 linear한 결과를(변하지 않는) 출력하기 때문에 사용한다고 한다.)
이러한 이유 ? 때문에 activation function 을 사용하여 input data를 변화시켜 준다.
4. Error 측정 ( Loss function 정의 )
Affine transformation 과 Activation function으로 변환을 거친 (N,1) input data는 shape이 같아 (N,1) label data와 비교가 가능해졌다.
흔히 많이 쓰는 대표적인 loss function 으로는 MSE(평균제곱오차) 와 cross entropy error(교차엔트로피 오차 ,정보이론에서 나온 걸로 생각됨 나중에 공부할 것)가 있다. 그 중 MSE를 예시로 들자면
 (내가 알기론 unbiased estimator 인 MSE는 자유도가 n-2 이므로 (n-2) 로 나눠줘야 하는데 데이터가 방대하니 그 차이가 미세하여 무시해도 좋을 정도로 판단하여 이렇게 정의한듯 하다.)
(내가 알기론 unbiased estimator 인 MSE는 자유도가 n-2 이므로 (n-2) 로 나눠줘야 하는데 데이터가 방대하니 그 차이가 미세하여 무시해도 좋을 정도로 판단하여 이렇게 정의한듯 하다.)
yi는 label data, ![]() 는 변환된 input data에 해당되어 그 차이를 제곱하여 다 더한 값이다. ( 제곱하면 양수가 되기 때문 )
는 변환된 input data에 해당되어 그 차이를 제곱하여 다 더한 값이다. ( 제곱하면 양수가 되기 때문 )
이 차이가 맨 위에서 말한 linear regression에서의 설명할 수 없는 요인을 추정할 수 있는 잔차(residual) 부분이다. 즉 오차 ε 의 추정량으로써 variance이다. 이 잔차의 분산을 minimize 하는 것이 이 model의 목표가 된다.
5. 학습 ( Gradient Descent)
오차의 분산을 minimize 할 때 (즉 오차의 분산을 0으로 만드는 것이 목표) , 실제로 0으로 만드는 것은 불가능?하다.
linear algebra 에서는 ![]() 라는 명시적인 해(근사해를 구하는 방법) 를 구하는 공식이 존재한다.
라는 명시적인 해(근사해를 구하는 방법) 를 구하는 공식이 존재한다.
(간단히 얘기하자면 우리가 사는 차원에서는 답을 만족하는 해를 찾을 수 없어서 그림자처럼 직교로 내려서 제일 가까운 근사치를 구하는 방법이다.)
하지만 이는 data들이 independent해야만 존재하는 해이므로 실생활에서는 적용하기 힘든 해이다. ( 실제로 모아 놓은 data들이 독립적인지 종속적인지도 판단하기 어려운 경우가 허다하다.)
(같은 얘기지만 )이를 통계학적인 방법인 최소제곱법으로 찾게되면 각 weight들에 대한 오차의 분산을 편미분한 값이 0이 되는 연립방정식의 해로 말할 수 있다.

하지만 b0, b1같이 간단한 두 개의 weight를 구하는 연립방정식의 해는 쉽지만 역시 우리가 현실에서 마주하는 data는 무수히 많은 weight를 가지기 때문에 동시에 0을 만족하는 방법은 불가능에 가까워진다.
Solution
(정리)우리는 loss function을 어떤걸 정할지 결정했고 (여기선 MSE를 선택) , 그 값을 최소화하는 (0으로 만드는 ) 방법은 각 weight들이 그 값에 대해 편미분하였을 때 = 0을 만족하는 연립방정식의 해를 구하는 것이다.
여기서 놀라운 생각하나가 튀어나오는데 이 방법이 Gradient Descent이다. 각 weight들을 편미분하였을 때 ( 함수식 = 0 으로 놓고 푼 것이 아니고 그냥 편미분하였을 때) 기울기들은 각 지점에서 낮아지는 방향을 가리킨다.(함수의 출력 값을 가장 크게 줄이는 방향)

그 방향이 정답이라고는 말할 수는 없으나, 그쪽으로 가야 함수 값을 줄일 수 있다. 여기서 가리키는 방향( 기울기 )으로 일정 거리만큼 이동해서 다시 기울기를 구하고, 이 작업을 반복하여 점차 낮은 곳으로 향해가는 방법이 경사법이다.
얼마만큼의 일정거리를 움직일 건지 정하는 건 우리들의 몫이고 (학습률이라 함) 이를 수학식으로 표현하면
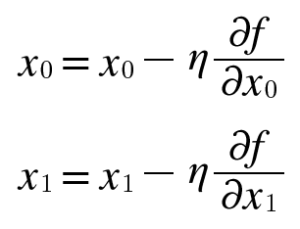 여기서
여기서![]() (에타) 는 우리가 정하는 학습률을 뜻하고 xo 와 x1 은 weight를 뜻한다. 조금씩 조금씩 해를 찾아 간다.
(에타) 는 우리가 정하는 학습률을 뜻하고 xo 와 x1 은 weight를 뜻한다. 조금씩 조금씩 해를 찾아 간다.
(오차역전파법은 나중에)
6. 평가 (evaluation)
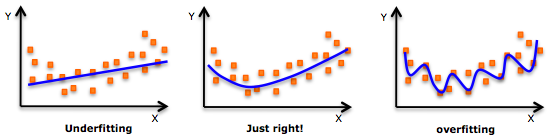
under fitting인 경우는 model의 자체가 잘 못됐을 가능이 크다.
over fitting인 경우는 model을 너무 섬세하게 학습했기에 어느정도 규제가 필요해보인다.