M.L (p.203)
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 |
# coding: utf-8 import numpy as np import matplotlib.pyplot as plt def sigmoid(x): return 1 / (1 + np.exp(-x)) def ReLU(x): return np.maximum(0, x) def tanh(x): return np.tanh(x) input_data = np.random.randn(1000, 100) # 1000개의 데이터 node_num = 100 # 각 은닉층의 노드(뉴런) 수 hidden_layer_size = 5 # 은닉층이 5개 activations = {} # 이곳에 활성화 결과를 저장 x = input_data for i in range(hidden_layer_size): if i != 0: x = activations[i-1] # 초깃값을 다양하게 바꿔가며 실험해보자! w = np.random.randn(node_num, node_num) * 1 #w = np.random.randn(node_num, node_num) * 0.01 #w = np.random.randn(node_num, node_num) * np.sqrt(1.0 / node_num) #w = np.random.randn(node_num, node_num) * np.sqrt(2.0 / node_num) #w = np.zeros((node_num,node_num)) #w = np.ones((node_num,node_num)) #w = np.full((node_num,node_num), 5) a = np.dot(x, w) # 활성화 함수도 바꿔가며 실험해보자! z = sigmoid(a) # z = ReLU(a) # z = tanh(a) activations[i] = z # 히스토그램 그리기 for i, a in activations.items(): plt.subplot(1, len(activations), i+1) plt.title(str(i+1) + "-layer") if i != 0: plt.yticks([], []) # plt.xlim(0.1, 1) # plt.ylim(0, 7000) plt.hist(a.flatten(), 30, range=(0, 1)) plt.show() |
위의 코드는 가중치 값들의 여러가지 초기화방법과 활성화 함수 3가지를 가지고 신경망 학습을 할 때 이런 초기화 값들에 의해 데이터의 분포가 어떻게 이뤄지는지 그래프로 보여주는 코드이다. 각 다섯개의 범주로 나오는 분포들은 코드를 보다시피 초기화된 가중치와 입력 값을 연산하고 그 결과를 활성화함수에 넣은 값을 5번 반복하는데 각 결과를 activations에 저장한다.
먼저 가중치를 표준 정규분포 * 1 즉, 그자체로 초기화하고 시그모이드 활성화함수를 사용하여 나온 결과 값이다.
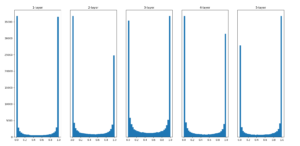 각 층의 활성화 값들이 0과 1에 치우쳐있다. 그 미분 값은 (오차 역전파 값) 시그모이드 함수(출력값 = y)는 y(1-y) 이기 때문에 0,1 출력 값이 각각 0(1-0) 과 1(1-1) 은 0. 그래서 미분이 0에 다가간다. 우리는 여기서 데이터의 분포가 0과 1에 치우치면 역전파의 기울기 값이 점점 작아지다가 사라지게 되는 것을 알 수 있다. 이 문제가 gradient vanishing(기울기 소실)이라 알려진 문제이다. 층을 깊게 하는 딥러닝에서는 심각한 문제가 될 수 있다. ( 미분의 값 이 0에 수렴하여 학습을 다 해도 값이 진전되지 못하고 끝난다. )
각 층의 활성화 값들이 0과 1에 치우쳐있다. 그 미분 값은 (오차 역전파 값) 시그모이드 함수(출력값 = y)는 y(1-y) 이기 때문에 0,1 출력 값이 각각 0(1-0) 과 1(1-1) 은 0. 그래서 미분이 0에 다가간다. 우리는 여기서 데이터의 분포가 0과 1에 치우치면 역전파의 기울기 값이 점점 작아지다가 사라지게 되는 것을 알 수 있다. 이 문제가 gradient vanishing(기울기 소실)이라 알려진 문제이다. 층을 깊게 하는 딥러닝에서는 심각한 문제가 될 수 있다. ( 미분의 값 이 0에 수렴하여 학습을 다 해도 값이 진전되지 못하고 끝난다. )
gradient vanishing 문제의 원인은 active function에 의존적이다?
active function (ex: sigmoid, Relu, tanh …)은 non-linear 한 function으로 넓은 input range들을 non-linear function의 작은 범위 (ex: sigmoid = -1 ~ 1)로 짓이겨 넣는다(squash). 이런 성질때문에 넓은 범위 input 값들이 잘 반영되지 못하고 작은 범위로 모아져 output 값으로 산출된다. 만약 첫 layer input에 대해 큰 변화가 있다 하더라도 잘 반영되지 못한다.
이어서 weight의 standard deviation 을 0.01로 바꿔 실행했다.
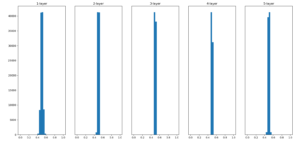 활성화 함수의 출력 데이터(은닉층의 활성화 값) 가 0.5 부근에 집중되어있다. gradient vanishing 문제는 일으키지 않았다만, 표현력 관점에서 큰 문제가 있다. 이 말은 다수의 뉴런이 같은 값을 나타내고 있기 때문에 뉴런이 여러개 있는 의미를 상실하게 된다. 예로 100개 뉴런이 1을 가리키고 있다면 1개의 뉴런이 1을 가리키고 있는 것과 별 차이가 없는 것이다. 그래서 활성화 값들이 치우치면 표현력을 제한한다는 관점에서 문제가 된다.
활성화 함수의 출력 데이터(은닉층의 활성화 값) 가 0.5 부근에 집중되어있다. gradient vanishing 문제는 일으키지 않았다만, 표현력 관점에서 큰 문제가 있다. 이 말은 다수의 뉴런이 같은 값을 나타내고 있기 때문에 뉴런이 여러개 있는 의미를 상실하게 된다. 예로 100개 뉴런이 1을 가리키고 있다면 1개의 뉴런이 1을 가리키고 있는 것과 별 차이가 없는 것이다. 그래서 활성화 값들이 치우치면 표현력을 제한한다는 관점에서 문제가 된다.
So. 각 층의 활성화 값들은 고루 분포되어 있어야 신경망 학습이 효율적으로 이루어진다.
가중치는 위의 초기화 (정규분포 * 0.01) 로 두고 활성화 함수를 Relu와 tanh(hyper tangent)로 바꾸어 돌려보았다.
Relu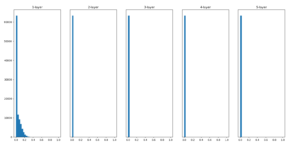
tanh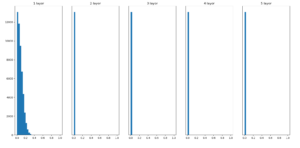
둘다 활성화 함수의 출력 데이터의 분포가 0에 분포하므로 gradient vanishing이 발생한다.