M.L (p.190)
Stochastic Gradient Descent method ( SGD ) 확률적 경사하강법
1.기능
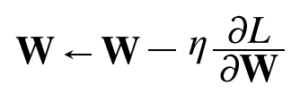W 는 가중치 매개변수이고 
(eta)는 학습률, 라운드디L / 라운드디W 는 손실함수의 기울기를 뜻한다. 즉 W값을 W에서 학습률 * 손실함수 기울기를 빼 그 값을 갱신한다.
|
1 2 3 4 5 6 7 |
class SGD: def __init__(self,lr= 0.01): self.lr = lr def update(self,params,grads): for key in params.keys(): params[key] -= self.lr * grads[key] |
SGD를 class 로 구현하여 모듈화시키면 어느때든 부를 수 있어 편리하다. 코드를 보면 학습률 lr = 0.01로 기본 값을 정의하고 update(params,grads)를 입력으로 받는다. params는 앞 신경망코드에서 초기화된 가중치,편향들이다. grads는 가중치와 편향들을 오차역전파하여 그 값을 저장한 변수다. 즉 params 변수에 학습률 * (오차역전파된 grads) 값을 -= 로 갱신한다.
2. SGD 단점
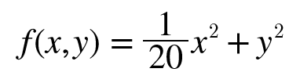편미분 f (x, y) = 1/20 * x² + y²
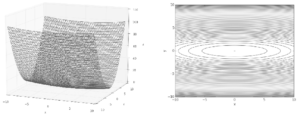
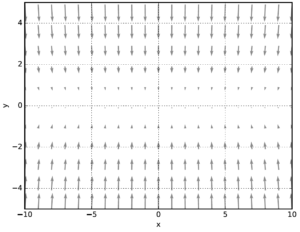
각 점에서 함수의 기울기는 (x/10, 2y)로 y축 방향은 가파른데 x축 방향은 완만하다. 또 최솟값은 (0, 0)이지만 기울기 대부분은 그 방향을 가리키지 않는다.
|
1 2 |
SGD는 비등방성anisotropy 함수(방향에 따라 성질, 여기서는 기울기가 달라지는 함수)에서는 탐색 경로가 비효율적이다. |
다음 글에서 해결법을 알아본다.
