M.L (p.167)

Sigmoid function 의 순전파와 역전파를 계산그래프로 이해해보겠다.

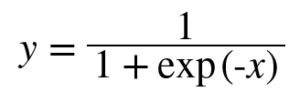sigmoid 식이다. 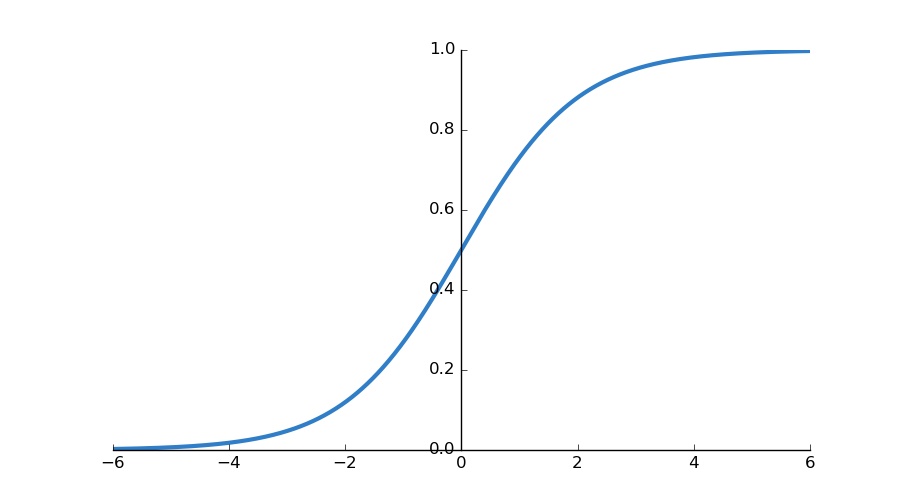sigmoidì ëí ì´ë¯¸ì§ ê²ìê²°ê³¼ 함수 그래프

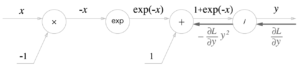순전파 식 전개

역전파 전개 : ‘∂(’라운드 디‘라고 읽음) 편의 상 ‘라운드’ 라 칭하겠다.

y = sigmoid로 치환하여 단순히 보자. 뒤쪽에서 라운드 L / 라운드 y 이 전파되어 왔고 / 노드를 계산해야한다. y = sigmoid = 1/x 로보자. 1/x 의 미분은 -1/x^2 이다. -x제곱 분의 1이다. 이제 y에 대입하여 만들어보면 -y^2 (-y제곱) 이 나온다.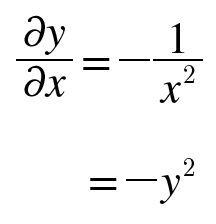

chain rule에 의해 -(라운드L/ 라운드 y) * y^2 이 된다.

+ 노드는 변화없이 그대로 흘려보내기 때문에 지나치고 exp(-x) 를 보자.

exp노드는 exp(x) 연산을 수행하고 미분 값도 자기 자신, exp(x)가 나온다.

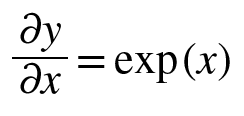그래서 처럼

-(라운드L/라운드y)*y^2* exp(-x) 가 된다. 이후 곱셈노드는 앞에서 본 것처럼

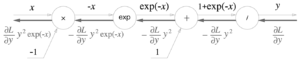
x에 대해서는 -1이 곱해지기 때문에 결과는 (라운드L/라운드y)*y^2* exp(-x)이 된다. 그런데 최종 출력 값이 출력y 와 입력x 로만 이루어진 식이기 때문에 우리는 중간과정을 모두 묶어 sigmoid 라는 노드 하나로 대체할 수 있다.

처럼 단순화할 수 있다.

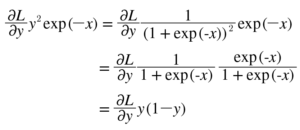로 정리되며 sigmoid 계층의 역전파는 순전파의 출력y 만으로 계산될 수 있다.

import numpy as np

class Sigmoid:
    def __init__(self):
        self.out = None

    def forward(self,x):
        out = 1 / (1 + np.exp(-x))
        self.out = out

        return out

    def backward(self,dout):
        dx = dout * (1.0 - self.out) * self.out

        return dx

import numpy as np

class Sigmoid:

def __init__(self):

self.out = None

def forward(self,x):

out = 1 / (1 + np.exp(-x))

self.out = out

return out

def backward(self,dout):

dx = dout * (1.0 - self.out) * self.out

return dx

Published by gjtrj55

답글 남기기 답글 취소하기