M.L (p.121)
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
import numpy as np import matplotlib.pyplot as plt def numerical_diff(f,x): h = 1e-4 return (f(x+h) - f(x-h)) / (2*h) def function_1(x): return 0.01*x**2 + 0.1*x x = np.arange(0.0, 20.0, 0.1) y = function_1(x) plt.xlabel("x") plt.ylabel("f(x)") plt.plot(x,y) plt.show() print(numerical_diff(function_1,5)) print(numerical_diff(function_1,10)) |
경사법에서는 기울기 값을 기준으로 나아갈 방향을 정하는데 기울기 값을 미분으로 구할 수 있다. (기울기 값이 0에 가까워지는 지점이 최적 값을 나타내기때문에 )
하지만 컴퓨터 상에서는 미분을 구할 때 limit 값을 표현하는 것에 문제가 있다. 1e-50 같은 수를 표기하면 반올림 현상 때문에 0.0으로 근사해버리므로 적절한 0.0이 되지않는 1e-4 ( 0.0001) 을 사용한다. 이렇게 근사해서 구하게 되는 수치미분 값은 실제 미분 값과 차이가 있기 때문에 그 차이를 최소화 시켜주는 중앙차분( 중심차분 )을 사용한다.
실제 0.01x^2 + 0.1x = function_1 을 중앙차분을 이용한 수치미분에 대입하면
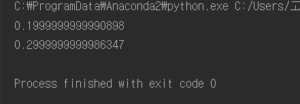x= 5, x = 10 일때, 0.2, 0.3 값에 가깝게 근사하여 나오는데 실제 미분값과 차이가 아주 미세하다.
