M.L (p.112)
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
import numpy as np y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0] t = [0,0,1,0,0,0,0,0,0,0] def mean_squared_error(y,t): return 0.5 * np.sum((y - t) ** 2) print(mean_squared_error(np.array(y),np.array(t))) y = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0] print(mean_squared_error(np.array(y),np.array(t))) |
mean squared error로
신경망을 학습시키는 방법으로
그 값이 작을수록 Error가 적다는 뜻으로 해석할 수 있다.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
import numpy as np def cross_entropy_error(y,t): delta = 1e-7 return -np.sum(t * np.log(y+delta)) t = [0,0,1,0,0,0,0,0,0,0] y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0] d = cross_entropy_error(np.array(y),np.array(t)) print(d) y = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0] d = cross_entropy_error(np.array(y),np.array(t)) print(d) |
다음 코드는 cross entropy error로
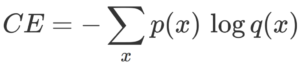
위의 함수이며 p(x) 는 정답레이블 q(x) 는 신경망의 출력이다. 이 때 p(x) 정답레이블은 one_hot_encoding 되어있어 0,1로 구성되어 있어 결과적으로 나오는 값은 정답레이블에 대응하는 신경망의 출력 값의 연산 값이 된다.
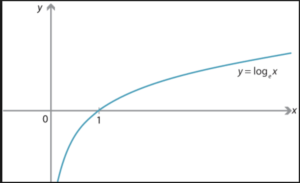위 결과 값의 그래프이며,
신경망의 출력 값이 정답레이블과 일치하는 확률이 높을 수록 함수 값은 0에 가까워지며 반대로 멀어질수록 – 무한대로 작아진다.
이처럼 음의 무한대로 작아지는 값에 의해 컴퓨터가 -inf로 출력을 하게되는 문제가 발생하는데 위의 코드에서 처럼 delta 값 (아주 작은 10의 -7승)을 넣어 이를 방지한다.
이처럼 출력 결과 정답에 근접한 값은 0.5를 정답에 비교적 멀리 있는 값은 2.3을 출력해주는 것을 볼 수 있다.
일반적으로 신경망을 학습시킬때 사용하는 loss function은 이 두 가지가 대표적이다.
